Tipler, Mosca; Física Para Cientistas e Engenheiros; 6ª Ed. - Capítulo 5, Seção 1, Questão 132.
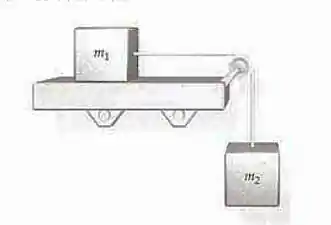
(Cap 5 – Ex 132) Um bloco de massa está sobre uma mesa horizontal. O bloco está preso a um bloco de ( através de um fio leve que passa por uma polia, sem massa e sem atrito, na beirada da mesa. O bloco de massa balança a do chão (Figura abaixo), O sistema é largado do repouso em e o bloco de atinge o chão em , O sistema é, agora, recolocado em sua configuração inicial e um bloco de é colocado sobre o bloco de massa Largado do repouso, o bloco de agora atinge o chão após . Determine a massa e o coeficiente de atrito cinético entre o bloco de massa e a mesa.
Passo 1
Falaaaaaaaaa galerinha do Responde ai, tudo joinha?
Bora resolver essa juntinho comigo?
Simboráaa
Os diagramas de corpo livre abaixo mostram as forças que atuam sobre os blocos cujas massas são e . No bloco 1, temos o peso, a normal, a tração no fio e a força de atrito. No bloco 1, só temos a tração e a força peso.
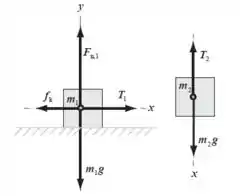
A aplicação da segunda lei de Newton e o uso da função horária do espaço nos permitirá encontrar uma relação entre o coeficiente de atrito cinético e .
A repetição deste procedimento com o bloco adicional no topo do bloco cuja massa é nos levará a uma segunda equação que, quando resolvida simultaneamente com a primeira equação, leva para uma equação quadrática em . Finalmente, sua solução nos permitirá substituir em uma expressão para e determine seu valor.
Passo 2
Usando a equação horária do espaço, podemos relacionar o deslocamento do sistema em sua primeira configuração em função de sua aceleração e tempo de queda:
Como a velocidade inicial é zero, isto é, :
Substituindo por valores numéricos:
A mesma expressão vale para a massa , já que para a massa 2 também, então:
Passo 3
Aplicando a 2° Lei de Newton no eixo x no bloco de massa , temos:
Substituindo por valores numéricos, temos:
Agora, aplicando a 2° Lei de Newton no bloco , no eixo x:
E no eixo y:
Passo 4
Usando a definição de força de atrito cinético e substituindo na primeira equação e multiplicando a segunda equação por do passo 3:
Agora, somando as duas equações:
Da mesma forma como vimos anteriormente:
Passo 5
Então, aplicando a 2° Lei de Newton no sistema, no eixo x, temos:
Substituindo o valor de que encontramos no passo anterior:
Simplificando essa equação, isto é, substituindo os valores que já temos, teremos uma equação de 2° em :
Substituindo na expressão de :