(Cap 4 – Ex 67) Uma caixa de massa está sobre uma estante horizontal sem atrito e presas por fios a caixas de massas e , como mostra a Figura 4-51. As duas polias são sem atrito e sem massa. O sistema é largado do repouso. Após a largada, encontre
(a) a aceleração de cada uma das caixas e
(b) a tensão em cada fio.
Passo 1
Faala, meu povo! Tudo bem com vocês? Partiu resolver mais um exercício?

Vamos começar com a análise do Exercício. Temos uma caixa em cima de uma superfície horizontal. Temos outras duas caixas presas nela. Uma à esquerda e outra à direita.
Só que a caixa à direita possui massa maior, portanto quando o sistema é retirado do repouso, a tendência é das caixas serem puxadas pela caixa de maior massa.
O exercício começa pedindo a aceleração de cada caixa. É interessante pensar nesses casos onde um objeto puxa o outro, já que a aceleração para todos os objetos será a mesma. Eles se movem juntos com uma distância constante entre eles (a cordinha no nosso caso). Se eles tivessem acelerações diferentes, por exemplo, se a caixa da direita tivesse maior aceleração, ela ia ter maior rapidez, se afastando da caixa do meio cada vez mais. Mas isso não é possível por causa da cordinha que tem sempre o mesmo comprimento.
Antes de partir para achar essa aceleração, precisamos criar o Diagrama de Corpo Livre de cada caixa para ter ideia de como as forças estão interagindo:
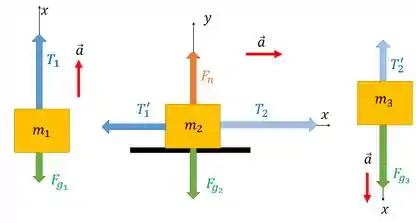
Colocamos no sentido da aceleração em cada caso só para facilitar as contas. Percebe que a aceleração é resultado de uma força resultante no seu sentido, por isso as força no sentido da aceleração aparecem maiores do que as que estão nos sentido inverso.
Temos tensões nos locais onde estão as nossas cordinhas. Cada caixa tem sua força peso por ter massa. E a caixa do meio tem uma força normal por estar em contato com a superfície.
O nosso objetivo, então, é equacionar essas forças através da segunda lei de Newton para achar .
Passo 2
Aplicando a segunda lei de Newton na caixa de massa na direção , temos:
Como está no sentido do eixo , ela aparece positiva no somatório, e o contrário acontece com :
Lembrando que :
Aplicando a segunda lei de Newton na caixa de massa , temos:
Aqui quem está no sentido positivo de é , que fica positiva no somatório e o contrário acontece com :
Como , porque é a mesma corda, temos que:
Aplicando a segunda lei de Newton na caixa de massa , temos:
Aqui quem está no sentido de é a força peso , por isso ela aparece com sinal positivo no somatório, o contrário de (que vai ter o mesmo módulo de ):
Passo 3
Como a aceleração do sistema é igual para todos os corpos, podemos relacionar as equações encontradas:
Podemos somar todas elas e simplificar:
Isolando quem queremos encontrar:
Substituindo os valores, temos que:
Passo 4
b) Queremos descobrir e .
Da equação , temos que
Substituindo os valores:
E da equação temos que
Substituindo os dados:
Se a Física não é a melhor matéria do mundo, então não sei qual é...
Para essa questão é isso pessoal! Bora resolver mais uma?

Resposta
a)
b)