Tipler, Mosca; Física Para Cientistas e Engenheiros; 6ª Ed. - Capítulo 5, Seção 1, Questão 3.
(Cap 5 – Ex 3) Um bloco de massa repousa sobre um plano inclinado em um ângulo de com a horizontal. Segue-se que o coeficiente de atrito estática entre o bloco e o plano é
(a)
(b)
(c)
(d) .
Passo 1
Olá, querido! Tá bem? Então, ele diz que um bloco está paradinho em cima de um plano inclinado. E pede uma relação entre o coeficiente de atrito estático (entre a superfície e o bloco) e a tangente de .
As forças que estão agindo no bloco são a força normal , a força peso e a força de atrito . As forças estão representadas abaixo:
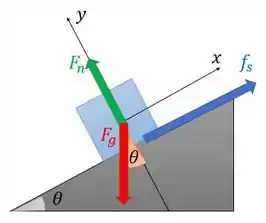
Sem a força de atrito, esse bloco iria deslizar para baixo por causa da força peso. Então ela deve aparecer como uma força que se opõe a esse movimento, por isso ela está no sentido de subir a rampa.
Vamos assumir o sistema de coordenadas como está indicado na figura acima. A única força que não está nos eixos é a força peso, então devemos decompô-la nos eixos x e y, dessa forma:
Colocamos o cosseno na componente porque que orienta está colado nesse eixo. Colocando essas componentes no nosso desenho:
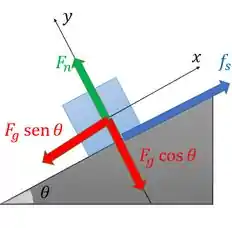
Passo 2
Como o enunciado fala, o bloco repousa no plano inclinado, então temos e . Por isso, a segunda lei de Newton:
fica assim para a direção do bloco:
A componente do peso fica negativa no somatório porque ela aponta para a parte negativa de .
E a segunda lei de Newton para a direção fica:
Novamente a componente da força peso fica negativa porque aponta para a parte negativa de .
Passo 3
Se dividirmos a equação por , obtemos:
Aí a gente precisa lembrar que o atrito estático máximo é dado por
Onde é o coeficiente de atrito estático entre o bloco e a rampa. Se ele é máximo, podemos escrever que ele é um teto para a nossa força de atrito estático
Substituindo a expressão dele:
Dividindo os dois lados por :
Lembra que achamos que , substituindo:
E isso é o que está escrito na letra d. 😊
Resposta
Resposta certa: (d)