O campo elétrico produzido por duas cascas cilíndricas co-axiais longas é representado pelas linhas de campo elétrico indicadas abaixo. A carga na casca cilíndrica interna é .
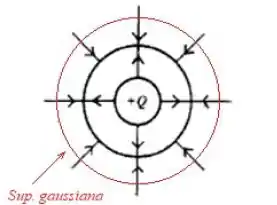
Das respostas abaixo a única opção que pode representar a carga na casca cilíndrica externa é:
zero
Passo 1
As linhas de campo elétrico estão entrando na superfície gaussiana, então podemos dizer que o fluxo elétrico é negativo . Se olharmos para a Lei de Gauss:
Vemos que, se , então . Onde representa a soma de todas as cargas no interior da gaussiana.
Passo 2
Sendo a carga da superfície (casca) interna, e a carga da superfície externa, temos:
Onde . Se reorganizarmos os termos:
Dentre as opções, a que representa essa possibilidade é a letra , onde .
Passo 3
Uma outra forma de resolver essa questão é observando as linhas de campo elétrico.
A Lei de Gauss nos mostra que o fluxo elétrico é proporcional à carga no interior da gaussiana:
Se fizermos uma gaussiana que fique localizada entre as duas cascas cilíndricas, veremos que ela apresenta um fluxo elétrico positivo, com 4 linhas de campo saindo dela.
No entanto, a superfície gaussiana que o problema nos deu tem um fluxo elétrico negativo, 8 linhas de campo entrando da mesma:
Dito isso, podemos concluir que:
Onde a carga será a soma da carga da superfície interna e da carga da superfície externa , que é justamente quem queremos descobrir. Logo:
Resposta