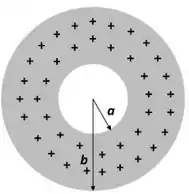
Numa esfera dielétrica oca existe uma densidade volumétrica de cargas constante. O raio externo da esfera é igual a e o raio do buraco esférico concêntrico é igual a , conforme a figura. Determine o fluxo elétrico através de uma gaussiana esférica concêntrica de raio .
Passo 1
Segundo a lei de Gauss, temos que:
onde é a carga total dentro da superfície fechada (superfície Gaussiana), dada por:
Na expressão acima, é o volume total, dado por:
Assim, o fluxo será dado por: