Determine o campo elétrico devido a uma fina casca esférica carregada de raio e carga total .
Passo 1
Nesse caso, a gente tem uma configuração de cargas que só depende da distância até o centro da casca esférica, então a gente tem aqui uma simetria esférica certo?
Isso quer dizer que deve ser radial e seu módulo só deve depender da distância até o centro.
Então vamos escolher pra esse caso uma superfície gaussiana esférica concêntrica à casca esférica e com um raio arbitrário beleza? Vamos ter algo parecido com essa imagem
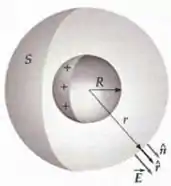
Agora temos que usar a Lei de Gauss e avaliar os casos em que e
Passo 2
A Lei de Gauss é expressada assim
Sabendo que o valor de é o mesmo em qualquer ponto da superfície gaussiana e que a área da superfície de uma casca esférica é , podemos escrever que
Devido à simetria, , então
Agora basta avaliar essa expressão quando e quando
Passo 3
Quando , a carga dentro da superfície gaussiana vai ser 0, então
Para , a superfície gaussiana engloba toda a casca esférica, então a carga dentro dela vai ser o próprio
Resposta
onde