Ache as equações nas formas vetorial, paramétrica e simétrica da reta que passa pelos pontos e .
Passo 1
O enunciado nos pede as equações da reta na forma vetorial, paramétrica e simétrica e simplesmente nos fala que a reta que queremos encontrar passa pelos pontos e . Mas, como vou escrever as equações se só tenho pontos??

Acho que já sei!!! Para determinar uma reta eu preciso do vetor diretor e de um ponto que a reta passa, certo? Corretíssimo!!!
Bem, eu tenho o ponto, mas falta o vetor diretor! O vetor diretor, nos dá a direção da reta! Perfeito!! E, como eu tenho dois pontos dessa reta, eu posso dizer que o meu vetor diretor é formado por esses dois pontos!!! Bingoo, é isso mesmo!! Como podemos ver na figura abaixo:
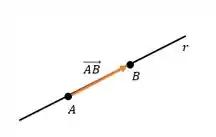
Passo 2
Então, vamos começar definindo o nosso vetor diretor que será ou . Tanto faz o sentido dos vetores, aqui não importa o sentido, mas a direção!! Escolhendo :
Definido o vetor diretor, vamos escolher um dos pontos ou para colocarmos nas expressões. Como eu gosto da letra , vou escolher essa para escrever as equações da reta. Você pode escolher o que não estará errado.
Agora, para determinar as equações é o mesmo processo que fizemos no exercício anterior. Mão na massa!!
Temos, que e como escolhi o ponto . Assim, nossa Equação Vetorial da reta, fica:
Passo 3
Agora, que já temos a equação vetorial escrever a paramétrica fica mais fácil ;). Como sabemos que o jeitão da paramétrica é:
Então, substituindo os valores, temos a Equação Paramétrica da reta:
Passo 4
Para fechar com chave de ouro, só falta a equação simétrica!!
Que é escrita assim:
Nosso e . Então, teremos:
Resposta
Equação Vetorial da Reta:
Equação Paramétrica da Reta:
Equação Simétrica da Reta: