Determinar o ponto de interseção das retas
Passo 1
O enunciado nos dá duas retas e e pede para determinarmos a interseção dessas duas retas. Como são retas, precisamos determinar o ponto em que as duas se cruzam.
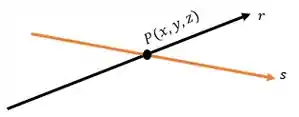
Pela figura devemos determinar o ponto . O ponto onde as retas se cruzam é o único ponto em que as duas retas tem em comum certo? Isso aí!!
Então, basta igualarmos as expressões das retas, a fim de achar as componentes de .
Passo 2
Vamos começar então!!! Primeiro vamos analisar as equações das retas dadas:
Aqui não precisamos nos preocupar em tentar descobrir em qual formato está cada equação, porque se você ver as equações da reta não estão em nenhum dos formatos de equações que vimos, masss, isso não importa ;). Pelas expressões da reta sabemos que deve valer . Pronto! Já temos um ponto de partida!
Passo 3
Agora, vamos substituir em todas as expressões tanto de como de .
Temos o seguinte sistema:
Com essas três equações devemos achar o valor de e . Subtraindo a equação da equação , temos:
Substituindo, na equação , temos:
Como, e devem ser valores válidos em todas as expressões e . Então, basta vermos se esses valores são satisfeitos pela equação .
Portanto, satisfaz, assim as retas se interceptam no ponto.
Importante: Se os valores encontrados não satisfizessem todas as equações, então, significaria, que as retas não possuem um ponto em comum, ou sejam, não se interceptam em nenhum lugar.