Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Introdução à Reta

Ver Teoria
Exercício 312456789101112131415

Enunciado

Obtenha equações paramétricas para os três eixos coordenados.

Passo 1

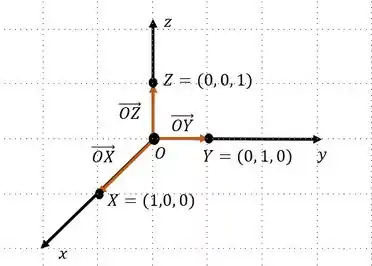
O enunciado quer que apresentemos as equações paramétricas de cada um dos eixos coordenados, ou seja, as equações paramétricas do eixo   x , do eixo y e do eixo z . Como vimos na teoria, para determinar uma reta, ou um eixo, que não deixa de ser uma reta, precisamos de um ponto pertencente à esta reta e seu vetor diretor. Para o caso dos eixos coordenados vamos analisar a seguinte figura:

Passo 2

Vamos começar analisando o eixo x .

Pela figura vemos que temos o ponto O que é a origem, então O = ( 0 ,   0 ,   0 ) e escolhemos o ponto X = ( 1 ,   0 ,   0 ) , e determinamos também o vetor O X → . Aqui, poderíamos ter escolhido qualquer outros pontos que pertencem ao eixo x , o fundamental é que o ponto escolhido esteja no eixo x . Assim, já temos o ponto e o vetor diretor do eixo   x , logo podemos determinar suas equações paramétricas, que serão determinados por:

X = 1 ,   0 ,   0 = x 1 ,   y 1 ,   z 1

O X → = X - O = 1 ,   0 ,   0 - 0 ,   0 ,   0 = 1 ,   0 ,   0 →   O X → = 1 ,   0 ,   0 = a ,   b ,   c

Então, as equações paramétricas do eixo x ficam:

x = 1 + 1 t y = 0 + 0 t z = 0 + 0 t → x = 1 + t y = 0 z = 0             ( t ∈ R )

Passo 3

Agora, analisando o eixo y . Pela figura determinamos o ponto Y = ( 0 ,   1 ,   0 ) e o vetor diretor do eixo y , O Y → = Y - O = ( 0 ,   1 ,   0 ) . Podemos escrever as equações paramétricas do eixo y :

x = 0 + 0 t y = 1 + 1 t z = 0 + 0 t → x = 0 y = 1 + t z = 0       ( t ∈ R )

Lembrando, que poderíamos ter escolhido outro ponto, desde que o mesmo esteja no eixo y . O mesmo podemos dizer do vetor diretor, poderíamos escolher outro, desde que os pontos que dão a direção do vetor, ambos, pertençam ao eixo y .

Passo 4

Para finalizar, o eixo z .

Novamente, pela figura temos o ponto Z = ( 0 ,   0 ,   1 ) e o vetor O Z → = Z - O = ( 0 ,   0 ,   1 ) . Com esses dados conseguimos determinar as equações paramétricas do eixo z .

x = 0 + 0 t y = 0 + 0 t z = 1 + 1 t → x = 0 y = 0 z = 1 + t           ( t ∈ R )

Resposta

Equações paramétricas do eixo x :

x = 1 + t y = 0 z = 0           ( t ∈ R )

Equações paramétricas do eixo y :

x = 0 y = 1 + t z = 0             ( t ∈ R )

Equações paramétricas do eixo z :

x = 0 y = 0 z = 1 + t             ( t ∈ R )

Exercícios de Livros Relacionados

Prove que a tangente `a parábola y=a x ² ² num ponto P é a bissetriz do ângulo F P ^ P 0 , onde F é o foco e P0 é a projeção ortogonal de P sobre a diretriz.
Ache as equações paramétricas para o segmento de reta de ( 10,3 , 1 ) a ( 5 , 6 , - 3 ) .
Determine as equações simétricas da reta que passa pelo ponto 1 , - 5,6 e é paralela ao vetor ( - 1,2 , - 3 ) .Determine os pontos nos quais a reta da parte (a) intercepta os planos coordenados.
A reta que passa pelos pontos ( - 4 , - 6,1 ) e ( - 2,0 , - 3 ) é paralela à reta que passa pelos pontos ( 10,18,4 ) e 5,3 , 14 ?
Encontre uma equação vetorial para o segmento de linha partindo de - 2,18,31 para ( 11 , - 4,48 ) .