Citar um ponto e um vetor diretor de cada uma das seguintes retas:

Letra

Temos as seguintes equações:

A primeira expressão tem a forma da equação simétrica da reta. Mas, e a segunda expressão está em qual formato? Bom, na verdade a segunda expressão só está desse jeito, porque o valor de é zero, e só podemos escrever na forma simétrica quando os valores de e são diferentes de ZERO. Então, é como se reescrevêssemos, da seguintes forma:

Nós escrevemos assim só para ficar mais fácil de acharmos o vetor diretor e o ponto , mas essa expressão não existe, pois não faz sentido a divisão por ZERO, beleza?! ;)

Então, comparando as seguintes formas:

Temos, que:

Esse item terminamos!!

Letra

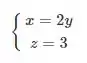
Temos duas formas de resolver!!

Primeira maneira:

A primeira equação está no formato da equação reduzida. E, a segunda também. Detalhe, que nessas equações reduzidas e são escritos em função de , as variáveis e são as coordenadas de um ponto que pertence à reta, então temos que:

Assim, se dermos valores para , acharemos pontos pertencentes à reta:

Com esses dois pontos conseguimos determinar o vetor diretor que pode ser ou . Escolhendo :

Assim, já temos dois pontos pertencentes à reta dada pelas equações reduzidas e o vetor diretor:

Segunda maneira:

Vamos começar da equação simétrica para então chegarmos na equação reduzida, onde devemos deixar e em função de

Isolando , temos:

Isolando , temos:

Comparando as expressões e com as equações dadas pelo enunciado, chegamos que:

Com , podemos dizer que e , pois o importante é respeitar a proporção. Da segunda expressão , podemos escolher e , que satisaz também a expressão, poderíamos, escolher outros valores, desde que a expressão seja satisfeita, não tem problema.

Assim, temos tudo o que precisamos:

Letra

As equações dadas são as equações paramétricas da reta, vamos só escrevê-la de uma forma diferente:

Comparando o formato geral, com o dado, temos:

Assim, temos tudo o que precisamos: