Assuma orientado e considere coordenadas de pontos dadas em relação a um sistema de coordenadas fixado em de base ortonormal e positiva.
Considere o triângulo de vértices . O comprimento da bissetriz interna desse triângulo relativa ao vértice é
a)
b)
c)
d)
e)
Passo 1
E aííí galera, tudo certo? Vamos lá matar esse probleminha
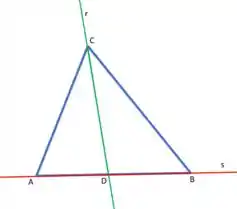
Temos esse triângulo aqui olha:
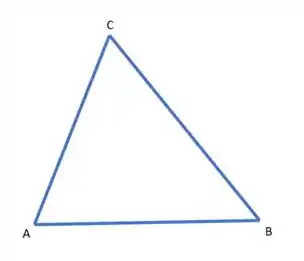
Onde . E aí queremos encontrar o comprimento da bissetriz interna em relação ao vértice .
A bissetriz interna vai cortar o ângulo em duas partes iguais. Ou seja, queremos o comprimento desse segmento verde:
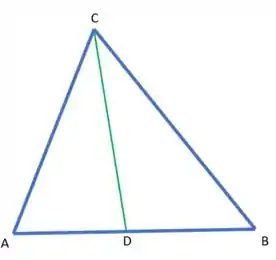
Então, tendo o vetor , queremos encontrar o módulo dele.
Para encontrarmos o vetor , precisamos encontrar o ponto . Esse ponto pode ser visto como a intersecção da reta da bissetriz com uma reta que passa por (a base do triângulo)
Encontrando essa intersecção, temos o ponto . E aí podemos encontrar o vetor e calcular o seu módulo. Vamos lá?
Passo 2
Vamos lá pessoal. Queremos encontrar o tamanho desse segmento verde:
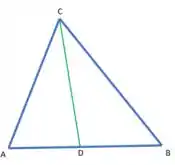
Vamos começar imaginando duas retas: uma () que é a continuação dessa bissetriz e outra () que passa pela base do triângulo
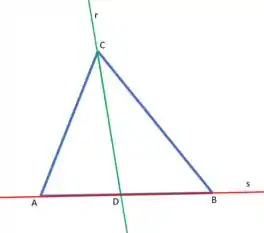
Como a reta divide o vértice em ângulos iguais, o seu vetor diretor pode ser escrito como
Onde
Então, um vetor diretor de é
Belezinha colega, já temos o vetor diretor da reta que forma a bissetriz 😉
Passo 3
Já temos o vetor diretor de , ele vai ser . E sabendo que a reta passa pelo ponto , uma equação pra ela é
Legal, mas isso ainda não é suficiente para encontrarmos o ponto . Precisamos da equação da reta também.
O vetor diretor de é o vetor , onde:
Sabendo que a reta passa pelo ponto , uma equação dela é
Ebaaa, já temos as equações das duas retas!
Agora vamos encontrar a intersecção entre elas para encontrarmos o ponto
Passo 4
O ponto é a intersecção entre as retas:
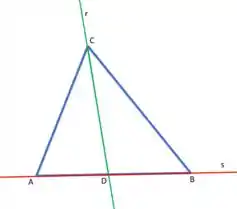
Para encontrarmos essa intersecção, basta igualarmos as equações das retas:
Então, igualando as coordenadas, temos esse sistema:
Boaa! Os valores de e que satisfizerem esse sistema vão ser os valores que dão o ponto de intersecção nas equações de e , respectivamente.
Da segunda equação, temos
Substituindo na primeira equação:
Substituindo na equação de , temos o ponto de intersecção das retas:
Logo, encontramos o ponto :
Passo 5
Agora que temos o ponto e o ponto , podemos encontrar o vetor . Ele vai ser:
Então, o tamanho do vetor vai ser:
Então
Ufa! Acabamos hahaha
Então a alternativa correta é a letra C

Resposta
c)