Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Modelagem com Equação do Calor

Ver Teoria
Exercício 1912345678910111213141516171820212223242526272829

Enunciado

UFMG, Sem campus, Equações Diferenciais B, P1- 2022.2, Questão 2c

Considere o problema de condução de calor:

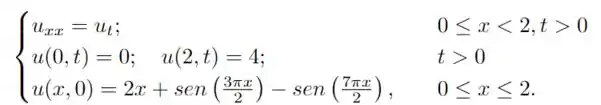
( c ) Encontre a solução do problema!

Passo 1

Oiiie, tudo bem com você?

Nós temos a construção usual de um problema de condução de calor em uma barra

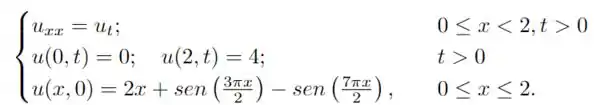
em que u ( x , t ) representa a temperatura ao longo do tempo t e ao longo do comprimento da barra x . Essa barra tem extremidades em x = 0 e x = L = 2 , e suas extremidades estão sendo mantidas à temperaturas u ( 0 , t ) = 0 e u ( 2 , t ) = 4 , além disso, sua distribuição de temperatura inicial ao longo da barra é u ( x , 0 ) = 2 x + s e n ( 3 π x 2 ) - s e n ( 7 π x 2 ) .

Na alternativa a ) encontramos a solução estacionária como

h ( x ) = 2 x

e a usamos na alternativa b ) para encontrar a solução transiente como

v ( x , t ) = s e n ( 3 π x 2 ) e - 9 π 2 4 t - s e n ( 7 π x 2 ) e - 49 π 2 4 t 2

Bem, agora só precisamos usar a definição

v ( x , t ) = u ( x , t ) - h ( x )

e, escrever a nossa solução! Vamos lá!

Passo 2

A solução é então dada por

u ( x , t ) = v ( x , t ) + h ( x )

ou simplesmente

u ( x , t ) = s e n ( 3 π x 2 ) e - 9 π 2 4 t - s e n ( 7 π x 2 ) e - 49 π 2 4 t 2 + 2 x

A questão foi isso! Te vejo na próxima! Tchau Tchau!

Resposta

u ( x , t ) = s e n ( 3 π x 2 ) e - 9 π 2 4 t - s e n ( 7 π x 2 ) e - 49 π 2 4 t 2 + 2 x

Exercícios de Livros Relacionados

Encontre a temperatura no estado estacionário u(ρ, φ) na esfera de raio unitário se a temperatura for independente de θ e satisfizer a condição de contorno:
Encontre a temperatura no estado estacionário em uma barra semi-infinita 0
Considere o fluxo de calor em um cilindro de comprimento infinito e raio 1: 0 ≤ r e as seguintes condições inicial e de contorno:Mostre que em que J0(λn) = 0. Encontre uma fórmula para cn.