Considere o problema de condução de calor:
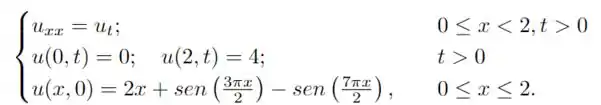
Encontre a solução transiente do problema.
Passo 1
Oiiie, tudo bem com você?
Nós temos a construção usual de um problema de condução de calor em uma barra
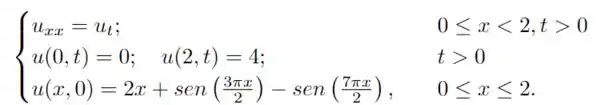
em que representa a temperatura ao longo do tempo e ao longo do comprimento da barra . Essa barra tem extremidades em e , e suas extremidades estão sendo mantidas à temperaturas e , além disso, sua distribuição de temperatura inicial ao longo da barra é .
Na alternativa anterior encontramos a solução estacionária como
usando essa solução vamos reescrever o problema dado em termos de um problema mais simples, o caso de condução de calor em uma barra com extremidades a mesma temperatura! Mas, como fazemos isso? Através da seguinte definição
Saca só o que acontece quando fazemos isso!
Passo 2
Substituindo a definição de em nossa equação diferencial, temos que
que é uma equação diferencial análoga à original do nosso problema. Mas, agora as condições de contorno são tais que
de forma que . Da mesma maneira, temos que
.
agora precisamos adaptar a nossa condição inicial
ou simplesmente
a solução do problema para nos dá a solução transiente desejada! Bora começar!
Passo 3
Okay, mas e agora? Como resolvemos o problema para ? Vamos usar o método de separação de variáveis, ou seja, vamos escrever que
ou seja, a solução é o produto de uma parte que depende apenas de , com uma parte que depende apenas de . Substituindo em nossa equação diferencial, temos que
se separarmos as variáveis, uma de cada da equação, temos que
note que igualei a uma constante negativa. Igualar a uma constante é padrão nas resoluções de equações diferenciais parciais por este método, já que se um lado evoluí dependendo apenas no tempo, e outro apenas na posição, a única forma de obter uma igualdade é se elas forem iguais a uma constante. Mas, porquê negativa? Isso é devido às condições de existência e unicidade da solução da equação diferencial! Você poderia colocar uma constante arbitrária, mas admitindo que ela é negativa, você economiza o trabalho de tentar obter outras soluções que não funcionam. As condições de contorno nos indicam que
como escolher que nos leva a solução trivial . Vamos escolher , pois isso nos leva à uma solução diferente! Da mesma forma, temos que
e temos . As condições iniciais do problema nós vamos tratar só no final! Vamos começar a resolver isso! Vem comigo!
Passo 4
A equação que comanda a distribuição da temperatura pela barra é
colocando tudo do lado esquerdo, temos a seguinte equação diferencial de segunda ordem homogênea
Isso nos leva ao seguinte polinômio característico
que tem raízes imaginárias da forma
Portanto, nossa solução é uma combinação linear de senos e cossenos da forma
Vamos aplicar as condições iniciais para encontrar as nossas constantes! Saca só!
Passo 5
Usando a condição inicial , temos que
obtemos que . Agora, da condição inicial , temos que
resultando na equação
se escolhermos , temos que , e portanto, . Isso é a solução trivial, portanto, vamos usar essa condição para colocar o seguinte vínculo na constante , temos que para zerar a equação acima, o argumento do seno deve ser
de forma que . Ou seja, temos uma solução para cada valor de , de forma que obtemos
Uff… Vamos resolver o lado direito da equação agora! Vem comigo!
Passo 6
O lado direito é a equação que depende do tempo
essa é uma equação diferencial de primeira ordem separável, se integrarmos ambos os lados na expressão acima, obtemos que
aplicando a exponencial em ambos os lados, podemos isolar como
Usando o valor de lambda que achamos anteriormente, temos que essa solução também é única para cada valor de na forma
Vamos achar agora a solução de nosso problema? Vem comigo!
Passo 7
A solução do nosso problema é o produto
mas note que a combinação linear de toda solução independente também é solução, portanto, a solução mais geral é da forma
Agora, finalmente podemos aplicar as nossa condição inicial , obtendo que
que nos leva à
note que do lado esquerdo podemos identificar os termos com e , e nenhum outro, portanto, a nossa soma é somente dada por
ou seja, comparando os dois lados, temos que e , e a nossa solução transiente é finalmente dada por
Guarde esse resultado pois precisaremos para a próxima alternativa! Te vejo jajá!