Exercícios de Modelagem com Equação do Calor - Lista de Exercícios Resolvida

Considere uma barra de alumínio com cm de comprimento, inicialmente a uma temperatura uniforme . Suponha que, no instante , a extremidade é esfriada a , enquanto a extremidade é aquecida a e ambas são mantidas, daí para frente, a essas temperaturas.

Encontre a distribuição de temperatura na barra em qualquer instante .

Considere uma barra uniforme de comprimento a uma temperatura inicial dada por , . Suponha que ambas as extremidades estão isoladas. Considerando , encontre a temperatura dessa barra.

Considere uma barra uniforme de comprimento , com distribuição inicial de temperatura , . Suponha que a temperatura na extremidade é mantida a , enquanto a extremidade está isolada, de modo que não há fluxo de calor através dela.

Encontre uma expansão em série para a temperatura da barra em função de .

Considere a condução de calor em uma barra de de comprimento com constante de difusividade térmica . Considere que a barra está apoiada sobre o eixo de modo a ocupar o intervalo . Suponha que a barra esteja termicamente isolada, inclusive nas extremidades, e que a temperatura inicial da barra seja dada pela função , . Encontre a temperatura que satisfaz as condições do problema, usando a expressão geral da solução do calor para uma barra isolada.

Considere a condução de calor em uma barra homogênea de comprimento igual a m e coeficiente de difusividade térmica igual a , cuja superfície lateral está isolada e que só troca calor com o ambiente através de suas extremidades. Suponha ainda que esteja inicialmente a uma temperatura de C e que a temperatura dos extremos da barra seja mantida constante igual a C para todo . Determine a temperatura sabendo que tal problema é modelado por

Resolva o problema

no caso seguinte:

Uma barra metálica de comprimento com constante de difusividade térmica é isolada termicamente, incluindo seus extremos. Suponha que a distribuição inicial de temperatura é onde:

Escreva a expressão da temperatura no instante .

Verifique que todas as soluções fatoradas da equação do calor da forma

que satisfazem as condições de fronteira que representam extremidades isoladas devem ser nulas.

Suponha que os extremos esquerdo e direito de uma barra homogênea são introduzidos em recipientes com líquidos a temperatura e , respectivamente. Utilizando a Lei de Resfriamento de Newton é possível deduzir que a densidade de fluxo de calor através das extremidades, deve satisfazer as igualdades:

onde e são constantes positivas que representam a condutividade térmica do material da barra e o coeficiente de transferência de calor, respectivamente entre o líquido e os extremos da barra.

Suponha que e são nulas, ou seja, ambos os líquidos estão sendo mantidos a temperatura zero.

c) Qual seria a maior dificuldade para resolver o problema em ?

Suponha que os extremos esquerdo e direito de uma barra homogênea são introduzidos em recipientes com líquidos a temperatura e , respectivamente. Utilizando a Lei de Resfriamento de Newton é possível deduzir que a densidade de fluxo de calor através das extremidades, deve satisfazer as igualdades:

onde e são constantes positivas que representam a condutividade térmica do material da barra e o coeficiente de transferência de calor, respectivamente entre o líquido e os extremos da barra.

Suponha que e são nulas, ou seja, ambos os líquidos estão sendo mantidos a temperatura zero.

Determine que condições de fronteira deve satisfazer para que uma solução fatorada da equação do calor satisfaça as condições de fronteira apresentadas acima.

Suponha que os extremos esquerdo e direito de uma barra homogênea são introduzidos em recipientes com líquidos a temperatura e , respectivamente. Utilizando a Lei de Resfriamento de Newton é possível deduzir que a densidade de fluxo de calor através das extremidades, deve satisfazer as igualdades:

onde e são constantes positivas que representam a condutividade térmica do material da barra e o coeficiente de transferência de calor, respectivamente entre o líquido e os extremos da barra.

Suponha que e são nulas, ou seja, ambos os líquidos estão sendo mantidos a temperatura zero.

d) Determine a solução estacionária do problema que você escreveu em (a).

Considere a condução de calor em uma barra de cm de comprimento, cujas extremidades, esquerda e direita são mantidas, respectivamente, a C e a C para . Suponha que inicialmente a temperatura ao longo da barra seja C. Considere .

1. Determine a temperatura de estado estacionário
2. Determine a expressão da temperatura para .

Considere a condução do calor em uma barra de comprimento cujas extremidades são mantidas à temperatura de para todo .

Em cada um dos casos a seguir, encontre uma expressão para a temperatura se a distribuição inicial de temperatura é a função dada. Determine se a condição inicial é satisfeita em todos os pontos e justifique. Explique em que sentido chamamos a expressão que você obteve de solução formal. Assuma que .

Considere a condução do calor em uma barra de comprimento cujas extremidades são mantidas à temperatura de para todo .

Em cada um dos casos a seguir, encontre uma expressão para a temperatura se a distribuição inicial de temperatura é a função dada. Determine se a condição inicial é satisfeita em todos os pontos e justifique. Explique em que sentido chamamos a expressão que você obteve de solução formal. Assuma que .

Considere a condução do calor em uma barra de comprimento cujas extremidades são mantidas à temperatura de para todo .

Em cada um dos casos a seguir, encontre uma expressão para a temperatura se a distribuição inicial de temperatura é a função dada. Determine se a condição inicial é satisfeita em todos os pontos e justifique. Explique em que sentido chamamos a expressão que você obteve de solução formal. Assuma que .

Considere a condução do calor em uma barra de comprimento cujas extremidades são mantidas à temperatura de para todo .

Em cada um dos casos a seguir, encontre uma expressão para a temperatura se a distribuição inicial de temperatura é a função dada. Determine se a condição inicial é satisfeita em todos os pontos e justifique. Explique em que sentido chamamos a expressão que você obteve de solução formal. Assuma que .

Verifique que para cada a função:

Satisfaz a equação do calor

Considere um reator submerso cujo núcleo é constituído de um número de placas verticais de espessura . Inicialmente o sistema possui temperatura uniforme e constante . Assume-se que a energia interna constante (considerada constante) é gerada uniformemente nestas placas. O coeficiente de transparência de calor entre as placas e os fluidos é dado por . A temperatura do fluido permanece constante e a espessura das placas é pequena quando comparada com as outras dimensões. Assim, se os efeitos de borda são desprezados, a transferência de calor pode ser assumida como unidimensional.

Nessas condições, o problema de condução de calor é dado por:

Onde é a densidade do material, é a capacidade térmica e é a condutividade térmica.

A solução no estado estacionário do problema acima é dada por:

Escolha uma opção:

a)

b)

c)

d)

Considere o problema de condução de calor:

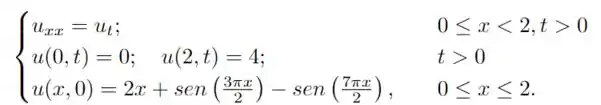
Encontre a solução do problema!

Considere o problema de condução de calor:

Encontre a solução transiente do problema.

Determine a solução de

Resolva o problema

, ;

;

(e)

Resolva o problema

, ;

;

(f)

Determine a solução estacionária do problema de condução do calor

Resolva o problema

onde e são constantes dadas.

Resolva o problema

, ;

;

(a)

Resolva o problema

, ;

;

(b)

Resolva o problema

, ;

;

(d)

Resolva o problema

, ;

;

(c)