Calcule a integral mudando a ordem de integração de forma apropriada
Passo 1
Vemos que o problema nessa integral não é a primeira integração, em , mas sim depois para integrar em , portanto vamos ter que mudar a ordem de integração, mas vamos manter a primeira integral em , vai ficar então .
Olhando os limites dados pela integral, vemos que o nosso sólido é definido por:
Nosso esboço fica:
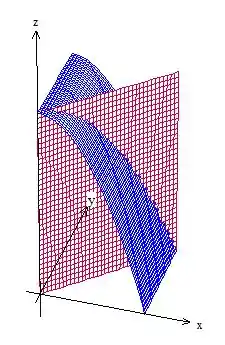
Passo 2
Como vamos manter a primeira integração em , podemos analisar somente o plano , nele tínhamos limitado por
E limitado por
No gráfico temos:
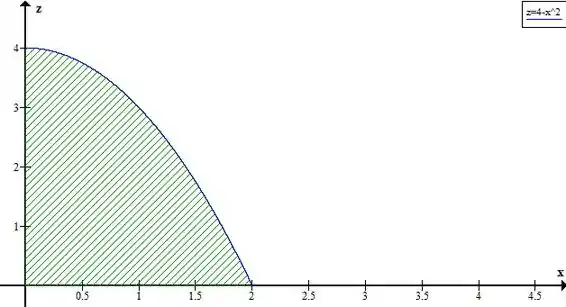
Invertendo a ordem de integração:
Como temos positivo, vamos somente considerar a raiz positiva:
Como não foi alterado, seus limites continuam
Passo 3
Colocando tudo na integral mudada, temos:
Passo 4
Integrando em
Integrando em
Integrando em