- Seja
Reescreva a integral na ordem .
Passo 1
Pow, infelizmente o sólido não nos está desenhado, por isso esse será o nosso primeiro trabalho aqui. Mas não se preocupe, pois tudo o que temos que fazer é pegar as informações de limites da própria integral. Veja!
Pow, principalmente desses dois primeiros intervalos tiramos superfícies muito importantes:
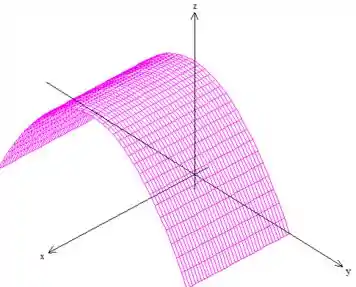
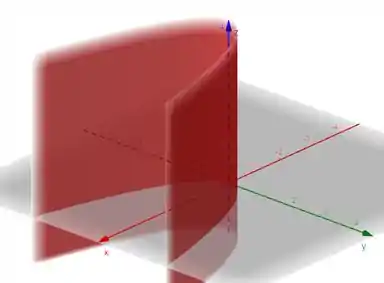
Que se desenharmos essas duas superfícies juntas, obtemos...
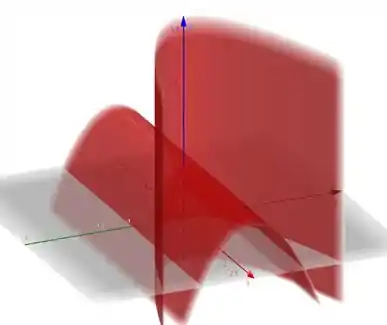
Esse já é basicamente o sólido que estamos trabalhando! Repare que ele está no primeiro octante, afinal de contas , e que é um cara positivo, sacou?
Passo 2
O que temos que fazer agora basicamente é mudar para a ordem indicada: .
Pensa comigo, se queremos o primeiro, então basicamente precisamos descrever esse sólido como do , onde temos que o deve variar entre superfícies.
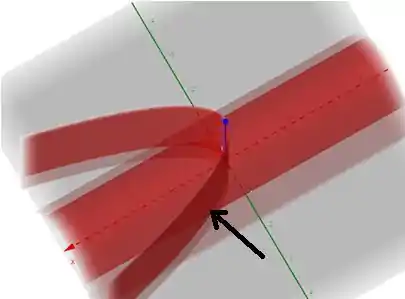
Se observar essa setinha preta, ela indica que o no sólido sai da parede e chega nessa superfície.
Como a superfície é , isolando ...
Quanto à variação de e , bem... Bora olhar a projeção desse cara no plano ! :D
Passo 3
Pow! esse tipo de projeção é bem easy de se fazer: basta que olhemos para o sólido, mas dessa vez como se colocássemos o nosso olho em cima do eixo e olhássemos de ladinho:
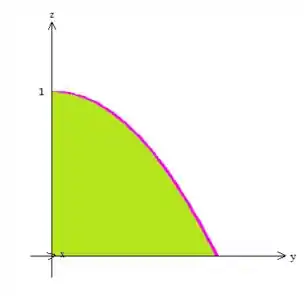
Repare que todo o sólido está preso pelo cilindro parabólico rosa... (que é esse pedacinho de parábola aí no plano ) e preso também no primeiro quadrante.
Mas enfim, temos que descrever essa região aí do tipo se quisermos , saca?
Então o é o cara que
Como a parábola é ... Isolando o :
Queremos a parte de cima apenas, então
Em relação a , bem, ele varia de até o ponto da parábola onde ...
Logo
Passo 4
Pow! Agora basta remontar a integral tripla considerando as novas variações
então