UFSC – Cálculo C – P1 – Questão 3
Descreva quatro outras ordens de integração distintas, além da ordem dada, para a integral
Passo 1
E aí pessoal, tudo bem? O problema nos deu essa integral tripla aqui
E pediu para invertermos os limites de integração de várias formas!
Mas você lembra como fazer isso?
Primeiro precisamos entender quais são as curvas delimitadoras, e isso a gente tira dos limites de integração:
Então estamos falando dessas curvas aqui
Então a ideia é selecionar uma variável para ir primeiro na integral, ver os seus limites pelas equações aí em cima. E depois as outras variáveis que sobrarem, fazer um esboço como elas são no plano que contenha só elas.
Mas relaxa, vou fazer passo a passo com você!
Passo 2
Começando por deixar em primeiro. As equações que levam ele são
Então esses são nossos limites!
Tranquilo até aqui?
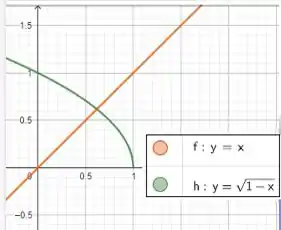
Igualando as duas equações podemos achar o ponto onde essas curvas se encontram,
Fazendo báskara e pegando apenas a raiz positiva! E isso será importante quando integrarmos na ordem , pois em temos uma quebra de limite de integração. Até a curva laranja é um limite e depois é outro!
Assim a ordem fica
Já em não precisamos quebrar! Pois , daí temos na ordem
Passo 3
Agora vamos deixar primeiro. Note que o limite mais interno fica o mesmo do enunciado
Agora temos que analisar o plano
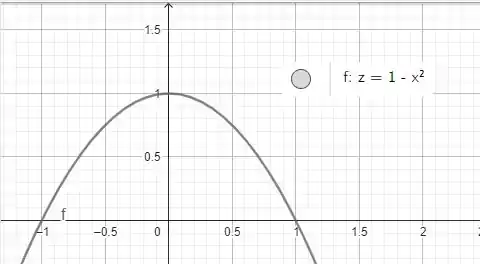então queremos a região apenas do primeiro quadrante:
assim a ordem fica
Passo 4
Por fim podemos analisar deixando o primeiro. Das equações temos que
E no plano
Então temos uma região retangular! E usando a ordem temos
E é isso! Encontramos quatro ordens diferentes de integração para essa integral tripla!
Tem outras! Você pode seguir na investigação!
Espero ter ajudado! Vamos para a próxima?