Questão 4: Considere o sólido limitado pelos planos , , e .
- Encontre as integrais iteradas que representam o volume do sólido.
- Calcule uma das integrais.
Dica: Faça um esboço do sólido.
Passo 1
Vamos seguir a dica do nosso problema então e começar desenhando a região! Esse sólido é formado primeiramente pelos planos e :
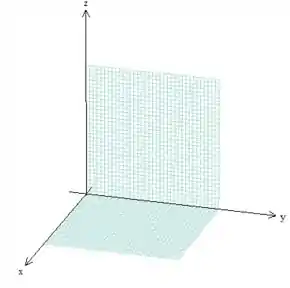
Em seguida a gente delimita mais um pouquinho desenhando o plano (se quiser desenha-lo bonitinho, sugiro primeiro fazer a reta no plano e depois “puxa-la” em direção ao eixo ):
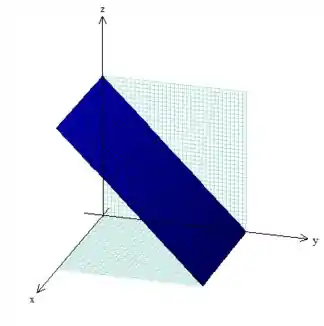
Por fim, devemos representar a outra base que é formada pelo plano (mesma dica anterior):
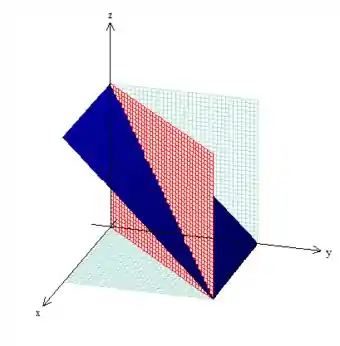
Veja o nosso sólido aqui então:
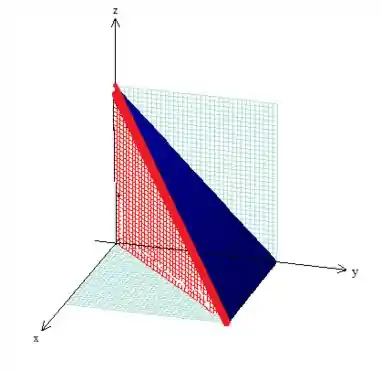
(ele é o um pedaço de tetraedro, por curiosidade )
Passo 2
Ok, para o primeiro item dessa letra, observe que queremos descrever o sólido necessariamente nessa ordem aqui:
Ou seja, devemos ter o variando entre funções que envolvem e . O deve variar entre funções de e o ... Deve variar entre constantes! Afinal é assim que podemos montar uma integral, se lembra?
Ok! Se o deve variar entre funções de e , então temos que dar uma olhada fixa para o nosso sólido e reparar que aqui o está variando entre uma base de e um teto formado pelo plano ...
Para a variação de e ... Bem! Acompanha-me! ;)
Passo 3
Já o e o , para facilitar, podemos olhar para a projeção do sólido no plano :
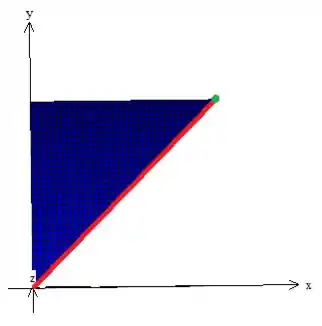
Veja que se quisermos ter o variando entre números, precisamos encontrar as coordenadas daquele ponto em verde. Veja que ele é a intersecção entre a reta e a reta , onde tiramos que...
Logo:
Enquanto o deve variar entre a base reta de até a reta ...
Passo 4
Ok! Então, com essas três variações, podemos montar a integral:
Passo 5
MAS AINDA TEM TRABALHO A FAZERMOS! Vamos agora vamos definir essa ordem aqui:
Ou seja, dessa vez o deve variar entre funções das outras duas variáveis, em seguida o deve variar apenas entre funções de , enquanto o continua variando entre números.
Veja no sólido que temos o variando da parede definida pelo plano vermelho, até ao lado do plano azul:
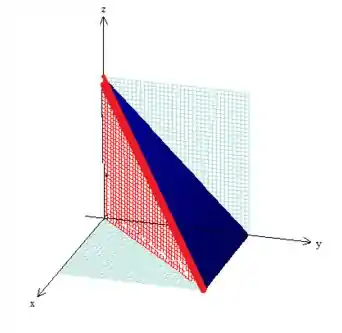
Ou seja:
Passo 6
Agora para descrever a variação de e , podemos olhar dessa vez para a projeção do sólido no plano ...
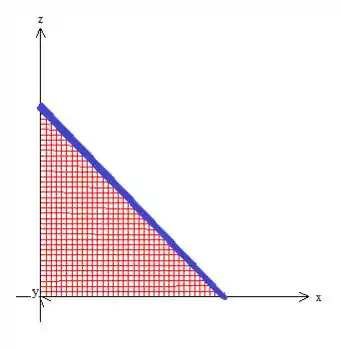
Veja que essa reta grossa na diagonal é formada pela sombra da intersecção entre os dois planos: o azul e o vermelho:
Logo, o varia dessa vez de até...
Enquanto isso, o continua variando de até :
Passo 7
Ok! Então, com essas três variações, podemos montar a integral:
Passo 8
Beleza! Então agora podemos escolher uma das integrais e calcula-las. Vamos com essa primeira aqui:
Calculando a integral de dentro...
Calculando agora a integral do meio...