UFSC, Sem Campus, Cálculo C, Provas Professor Saeger - P1 2022.1, Questão 3
Obtenha (quatro) outras ordens de integração distintas, além da ordem dada, para a integral
Passo 1
Oiie, tudo bem com você?
O enunciado nos dá a seguinte integral múltipla
e pede para achar outras ordens de integração. Mas o que quer dizer isso? Quando estamos trabalhando com integrações múltiplas devemos tomar um certo cuidado com a ordem de integração, note que os limites apresentam funções de , isso é um indicativo da região na qual está sendo realizada a integração, alterar a ordem, alterar esses limites, então, vamos tentar visualizar a nossa região e encontrar outras ordens possíveis! Saca só!
Passo 2
A ordem que estamos integrando agora faz inicialmente a integração em , desde o plano até o plano , em seguida, parte do plano até o parabolóide , por último fechando a região saindo do plano até o plano . Note que isso descreve o volume da seguinte região
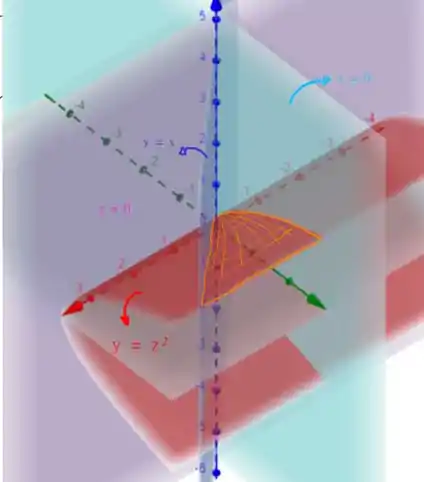
O tracejado laranja é a parte de baixo da região, ela é tampada pelo plano . O segredo aqui, é descrever essa região de outras maneiras!A primeira mudança que podemos fazer é sair primeiramente do plano até o parabolóide , e então partir de até intersecção do plano com o parabolóide , de forma que temos
Vamos procurar por outras agora!
Passo 3
E se quisermos integrar primeiro em Aí teríamos que partir do parabolóide , ou neste caso, até o plano que é a nossa tampa, então, eu posso partir do plano até o plano , e finalmente integrar em desde o plano , até a interseção do parabolóide com o plano , que é dado por , essa integral será
Ainda precisamos de mais duas! Vamos continuar integrando primeiro em , portanto, partindo de até . Mas, podemos agora partir primeiro do plano até a interseção de com , ou seja, . Por último, partimos de , até a interseção de com , portanto, a nossa integral se torna
Acha que já pegou o jeito? Falta só uma! Vamos fazer ela no próximo passo!
Passo 4
Vamos agora voltar a integrar primeiro em , portanto, como no enunciado, temos que sair do plano até o plano , mas agora, vamos integrar em , portanto, temos que partir do parabolóide , como fizemos no passo anterior e ir até o plano . Por último iremos integrar em , partindo de até a interseção de com , obtendo finalmente
Todas estas quatro são ordens válidas de integração! Se quiser verificar, faça e calcule o volume! Verá que o resultado será sempre que é o volume de nossa região! A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
Ao longo dos Passos!