Integrais duplas sobre regiões gerais
Considere a região do espaço definida por
E seja a fronteira de .
a) Esboce .
b) Determine usando igualdades e desigualdades.
c) Calcule o volume de .
Passo 1
a) Vamos lá, para esboçar essa região, basta desenvolver cada desigualdade. Para a primeira temos:
Ou seja, se temos a superfície , estamos na região dentro dela :D
Mas que superfície é essa?
Veja que, se zerarmos a variável , teremos uma circunferência centrada na origem, no plano . Se zerarmos a variável , teremos a hipérbole , no plano . E, zerando a variável , teremos a hipérbole no plano . Assim, o que temos aqui é o hiperboloide de uma folha centrado na origem:
Passo 2
Vamos agora às outras desigualdades? Para a segunda, teremos:
Ou seja, tendo a região dentro do hiperboloide, estamos tratando apenas do “tronco” entre e !
E, pela última desigualdade, teremos:
Isso significa que estamos pegando apenas metade dele, ou seja, a metade que tem positivo! O esboço de , portanto, fica:
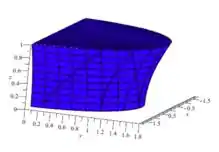
Passo 3
b) Vamos à próxima! Agora querem a região de interseção entre e o conjunto de pontos dado por:
Esse conjunto é uma superfície, certo? Ela é
Como representa um volume, e estamos fazendo sua interseção com essa superfície, então o resultado será outra superfície, beleza?
Se você reparar, essa é a mesma equação da superfície que contorna , não é? Exatamente! Então, se fizermos a interseção de com seu próprio contorno, teremos:
Viu como é singela a diferença? É praticamente a igual, só que dessa vez só temos o contorno de :D
Passo 4
c) Show, agora só falta calcular o volume de ! Como aquele hiperboloide que tínhamos era um amontoado de discos, um em cima do outro, e a região é a metade do volume desse hiperboloide, então só temos que resolver a integral:
Ou seja, vamos integrar entre e os discos de área , e, depois, dividir esse resultado por !
Agora só temos que encontrar esse raio ao quadrado em função de ... Veja, se temos o hiperboloide:
E, para cada circunferência, temos , então já temos que ! E a integral fica:
Integrando em relação a , teremos:
E aí está, o volume é !!
Resposta
a)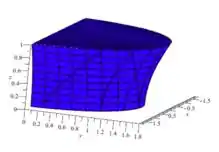 
b)
c)