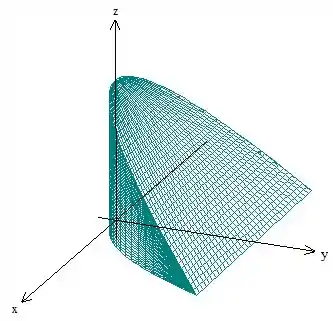
Esboce o gráfico associado à seguinte integral:
Passo 1
Vamos especificar primeiro os limites que podemos tirar a partir das integrais. Pela integral de fora:
Pela integral do meio:
Pela integral de dentro:
Passo 2
Vamos analisar os nossos dois primeiros limites. Perceba que eles estão no plano sendo que, em , vamos ter essas duas curvas:
Graficamente isso fica assim:
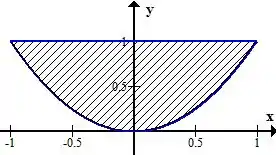
Passo 3
Tendo determinado a região em duas dimensões, vamos expandi-la para a terceira, no nosso caso, o eixo .
Pelo passo 1, vemos que está limitado pelos planos e . Em três dimensões e limitados pela região encontrada no temos o seguinte:
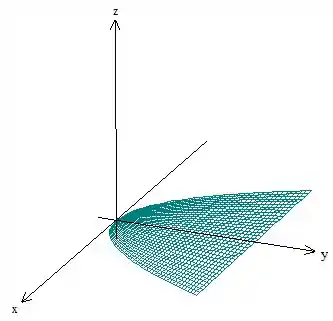
Agora para o plano também limitado por aquela região em :
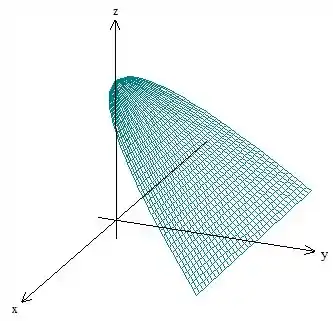
Perceba que ambos os planos existem em outros pontos, só que só queremos a região expandida em relação àquela encontrada no !
Pronto, agora é só ver qual o sólido que está entre essas regiões. Fica assim:
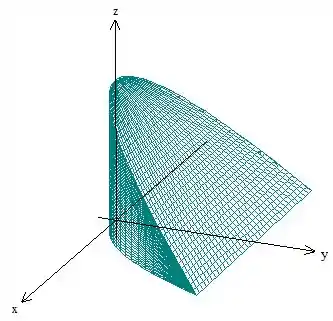
Resposta