Questão 4: Considerando o sólido
Resolva o que se pede:
b) Calcule o volume de .
Passo 1
Para o volume, podemos sempre calcular uma integral tripla dessa forma aqui:
Bem, normalmente é recomendado desenhar o sólido primeiro, porém isso está muito fora de questão aqui, afinal veja que uma das superfícies é (e não fazemos a menor ideia de quem seja esse cara). Contudo isso não é tão importante aqui, pois nós temos o sólido já bem descrito em termos de intervalos para as variáveis:
Podemos então escrever a integral tripla lembrando-se da ordem: O intervalo mais externo vem o intervalo numérico. A integral do meio pertence aquele que varia entre funções de uma única entre variável, e mais interna fica sendo...
Cuidado! A integral sempre DEVE ser montada dessa forma como explicado, ok? Então vamos calcula-la?
Passo 2
Começando pela integral de dentro...
Se fossemos calcular essa próxima integral de dentro, veja nos daríamos com um problema:
Veja que não existe nenhum método conhecido, até agora, que a gente poderia utilizar para resolver essa integral do meio em . Mas calma, esse problema talvez pode ser resolvido (e vai) se fizermos uma mudança na ordem de integração!
Passo 3
OK! Mas a gente não pode fazer uma mudança de qualquer forma. Para fazê-la, antes é necessário desenhar a região. Ai você poderia me perguntar:
“Mas a gente não ia deixar de desenha-la porque ela é muito complicada?”
NÃO!!! Tome cuidado, pois o que é muito complicado de se desenhar é o SÓLIDO E. O que vamos desenhar não é o sólido, e sim a região de variação das variáveis e . Para fazer isso inclusive, lembremos que...
Veja que dessas inequações, tiramos equações importantes:
A qual as três equações nos representa essa retas aqui:
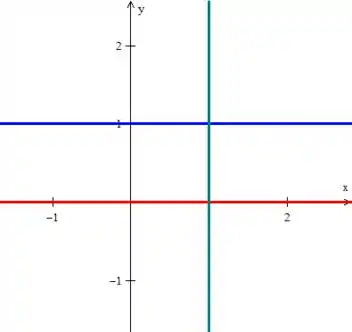
Enquanto ...
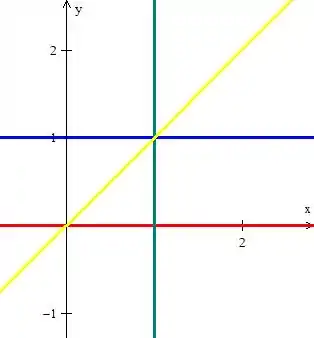
Logo, a região de variação de e se encontra no interior de todas essas retas:
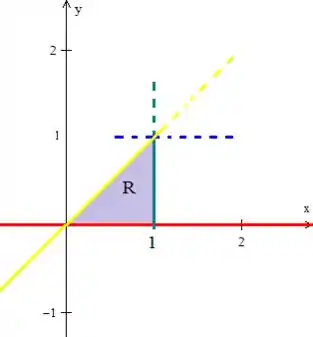
Passo 4
Bem, o que vamos fazer agora é basicamente escrever essa região, mas de forma diferente: ao invés de ter variando entre números, vamos pegar o fazendo esse papel:
Enquanto o , no caso, agora fica variando da base até a reta :
Logo, a gente pode voltar a integral e trocar os intervalos, bem como inverter a ordem de interação:
Agora podemos continuar a integral! Vamos lá?
Passo 5
Integrando agora em relação a e considerando como uma constante...
Agora, finalmente, conseguimos calcular essa integral fazendo uma mudança:
Trocando também os limites...