Considere . Seja a região espacial
E seja a fronteira de .
- Esboce
- Esboce
Passo 1
a)
Em questões de superfícies, o primeiro passo é sempre identificar com qual tipo de superfície estamos lidando. Em , temos:
Isso lembra muito a equação de uma esfera né?
A inequação também pode ser escrita como
Temos então uma superfície entre esferas, uma de raio e outra de raio . Na verdade, como e , vai ser um pedaço dessa superfície.
Passo 2
Vamos dar uma olhada nessas esferas (atenção, são apenas as cascas), a de raio 1 (em vermelho), e a de raio 2 (em azul claro):
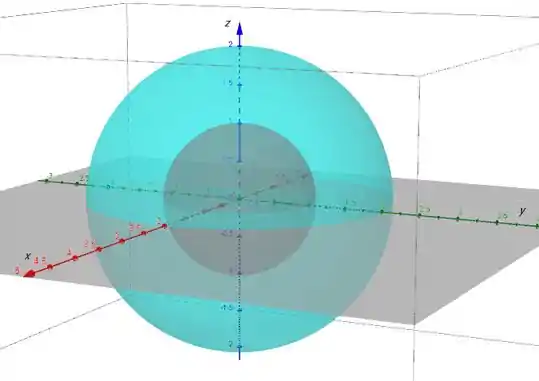
Agora, se determinarmos e vamos ter:
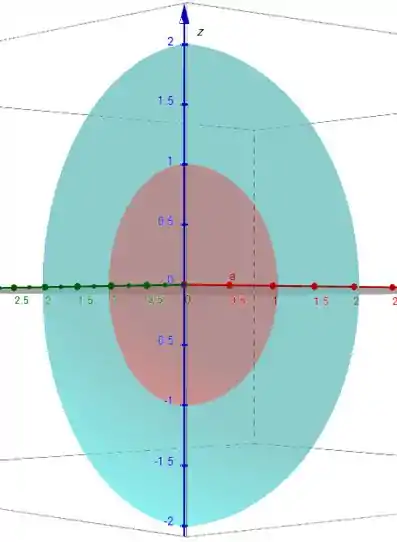
Ou, vendo de lado:
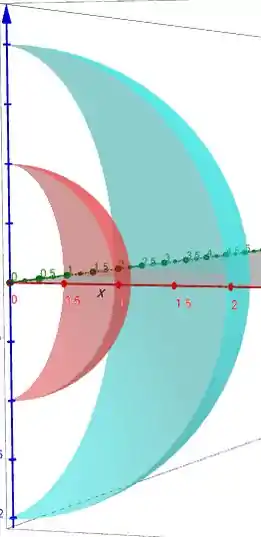
Nessa figura dá pra ver bem que as esferas são vazias, só temos as cascas. E a superfície é a região entre essas duas cascas.
Então a região é algo dessa forma:
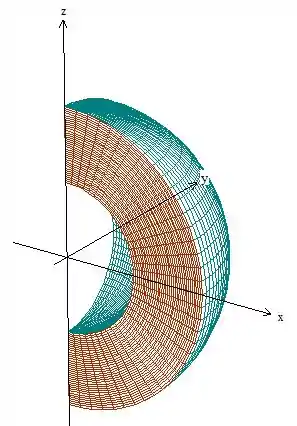
Vamos entender agora como é a região
Repara que ela é a interseção de com a esfera , então vai ser só a superfície da esfera de fora. Vamos ter
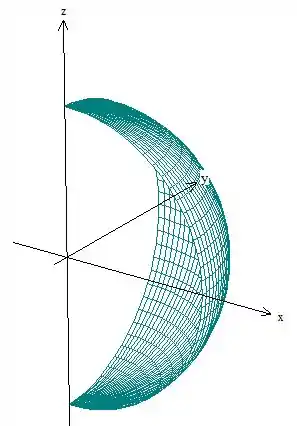
Pode ser difícil de esboçar, eu inclusive tenho bastante dificuldade com isso!
Mas têm esboços piores que esse: aqui basicamente a gente tem que tentar desenhar uma esfera de raio 2 centrada na origem e apagar dela, deixando só onde e são positivos! Tá, também não é muito fácil... Mas com prática fica melhor! :) Enfim, o esboço seria essa figura aí de cima.
Passo 3
b)
Vamos entender agora como é a região
Repara que ela é a interseção de com o plano , então vai ser só a parte vermelha que vimos do gráfico de , ou seja, é o plano que está dentro das esferas. Facilitaram nossa vida, agora só vamos trabalhar com 2 dimensões! Vamos ter
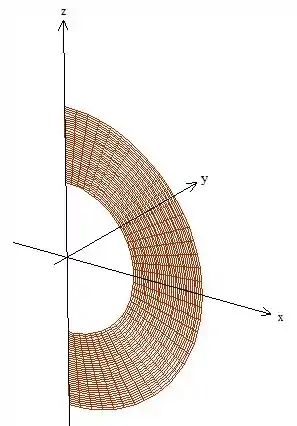
Ou:
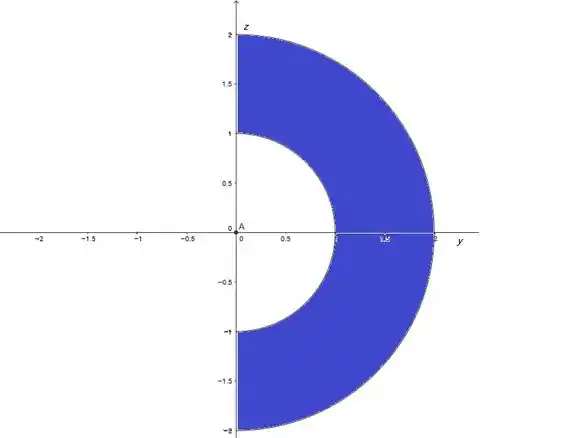
Resposta
Ei, a resposta está no passo a passo :)