Integral Dupla sobre regiões mais gerais
Considere a região espacial
- Seja a parte da fronteira de que está no plano
- Descreva usando desigualdades
- Calcule a área de
Passo 1
Ele começou dizendo que, em , vamos ter . Sabemos que , vamos substituir os valores de na desigualdade de , vamos ter
Podemos escrever como
Passo 2
Antes de fazermos a área, vamos entender o que é a região , ela vai ser o plano limitado por , indo de à . O gráfico fica
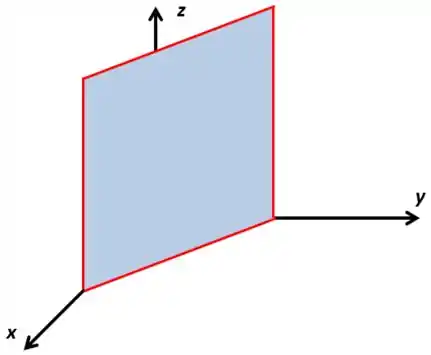
Isso vai ser um retângulo com base sendo a distância entre os pontos que esse plano corta o eixo e , e a altura sendo . Vamos descobrir as coordenadas desses pontos
Eixo , vamos ter
Eixo , vamos ter
Então a base vai ser a distância entre e , chamando essa base de
A área vai ser
Resposta
Exercícios de Livros Relacionados
Calcule a integral iterada.int_0^1 int_0^y int_x^1 6 x y z d z d x d y
Esboce o sólido cujo volume é dado pela integral iterada. ∫ 0 1 ∫ 0 1 - x ∫ 0 2 - 2 z d y d z d x
Escreva cinco outras integrais iteradas que sejam iguais à integral iterada dada. ∫ 0 1 ∫ y 1 ∫ 0 y f x , y , zd z d x d y
Expresse a integral ∭ E f x , y , zd V como uma integral iterada de seis modos diferentes, onde E é o sólido limitado pelas superfícies dadas. y = x 2 ,z = 0 ,y + 2 z = 4
Escreva cinco outras integrais iteradas que sejam iguais à integral dada. ∫ 0 1 ∫ y 1 ∫ 0 z f x , y , zd xd zd y