UFSC – Pré Cálculo – Lista 2 – Questão 24b
Em cada um dos itens abaixo, coloque as frações em ordem crescente:
Passo 1
Oi pessoal, tudo bem? O problema nos deu várias frações:
E pediu para colocarmos em ordem crescente. E agora? Você sabe como resolver?
Quando temos uma série de frações e queremos colocá-las em ordem precisamos que elas estejam com o mesmo denominador! Assim, se quisermos colocá-las em ordem crescente e os denominadores forem iguais, é só ordenar pelo numerador: nesse caso, do menor para o maior. Ok?
Para isso precisamos encontrar o dos denominadores! Assim podemos construir frações equivalentes com o mesmo denominador! E como encontrar o ?
A sigla significa , então queremos determinar qual é o menor número que é múltiplo tanto de quanto , ou seja, ao mesmo tempo de todos os denominadores das frações dadas
Mas calma, temos um algoritmo que nos ajuda a determinar isso! Você vai seguir os seguintes passos:
- Fatorar os dois números em números primos
- Fatore até chegar em , todos os números
- O será a multiplicação dos fatores primos!
Tranquilo?
Mas relaxa, vou fazer passo a passo com você!
Passo 2
Nossas frações são
Vamos encontrar o entre e :
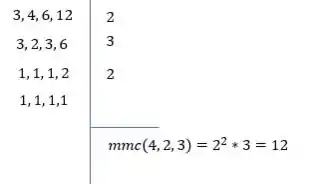
Tranquilo até aqui?
Passo 3
Agora vamos encontrar as frações equivalentes com o denominador . A gente encontra o numerador correspondente fazendo a operação proporcional ao que foi feito embaixo.
Precisamos encontrar as frações equivalentes a essas aqui:
Vamos começar com . Precisamos que o denominador seja , então o denominador de passou para , ou seja, fizemos embaixo: precisamos fazer a mesma operação em cima
Beleza?
Agora vamos reproduzir esse raciocínio para as outras frações! Para
Agora para :
E por fim para :
Para :
E por fim para :
Assim as frações reduzidas a um mesmo denominador ficam:
Passo 4
E agora por fim vamos ordená-las de forma crescente:
E é isso!
Espero ter ajudado! Vamos para a próxima?