Um astronauta a bordo de um ônibus espacial afirma que pode resolver com dificuldade dois pontos sobre a superfície da Terra, abaixo. Calcule:
- A separação angular dos pontos
- A separação linear dos pontos
Suponha condições ideais. Tome como o comprimento de onda da luz e como o diâmetro da pupila do astronauta.
Passo 1
Letra a)
A separação angular mínima para o astronauta resolver dois pontos com dificuldade é, usando a aproximação de pequenos ângulos:
O comprimento de onda da luz é e o diâmetro da pupila é . Substituindo:
Que é a separação angular dos dois pontos.
Passo 2
Letra b)
Para acharmos a separação linear entre os pontos, já tendo o ângulo entre eles, podemos usar a tangente do ângulo.
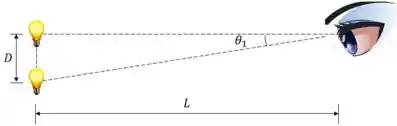
Onde é a separação linear dos pontos e é a distância do astronauta até os pontos na Terra.
Substituindo:
Resposta
Letra (a)
Letra (b)