Uma fonte de luz coerente e monocromática de comprimento de onda é utilizada num experimento cuja montagem está esquematizada na figura abaixo. As distâncias entre os anteparos consecutivos é . Luz incide normalmente sobre o anteparo , que possui duas fendas e , com mesma abertura e separadas por um distância . A distância é tal que os primeiros máximos laterais de interferência se localizem sobre as fendas e do anteparo . Elas possuem a mesma abertura das fendas do anteparo , mas estão separadas por uma distância .

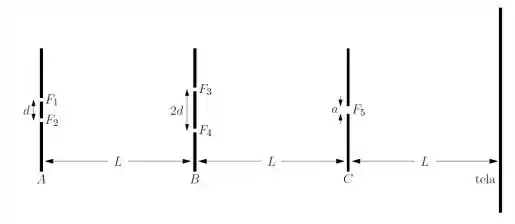
a) Quais são as diferenças de fase entre as ondas provenientes de e quando atingem as fendas e ?

b) Qual é o valor da separação em milímetros?

c) Qual é o valor limite da abertura (em milímetros) da fenda para que se possa distinguir dois máximos de difração (provenientes das fendas e ) na tela?

Agora vamos ao item (b). Sabemos que a interferência construtiva de duas fendas cuja distância é é dada por

Vamos olhar para o triângulo a seguir:

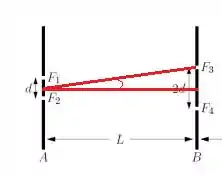
Temos que

Como , podemos usar a aproximação de pequeno ângulo:

Assim,

Substituindo na primeira equação

Além disso, como se trata do primeiro máximo lateral, temos que :

Portanto,

Ou ainda,

Vamos finalizar com o item (c). Nós queremos achar o valor limite da abertura da fenda para que se possa distinguir os máximos de difração provenientes da interferência entre as fendas e . Sabemos que o ângulo limite é dado por

Por outro lado, como a distância entre as fendas é e a distância entre os anteparos é , temos que

Usando a aproximação de ângulos pequenos novamente:

Assim,

Portanto,

Ou ainda,