Uma fenda estreita é iluminada por uma fonte monocromática puntiforme a uma distância da fenda, produzindo uma figura de difração sobre uma tela distante de da fenda.
A distância entre os mínimos adjacentes ao máximo principal nessa figura é de .
- Se a largura da fenda for duplicada, qual será a nova distância entre os mínimos adjacentes ao máximo principal na figura de difração? Justifique sua resposta.
- Nas condições do enunciado, uma segunda fonte puntiforme , idêntica mas não coerente com a primeira fonte, é colocada a uma distância da fonte original, paralelamente à direção da largura da fenda.
Qual é o menor valor de para que ainda seja possível identificar pela figura de difração na tela a presença de duas fontes distintas?
Passo 1
Letra a)
A distância entre dois mínimos adjacentes é:
Onde é a distância da fenda até o anteparo, é o comprimento de onda da luz e é a largura da fenda.
Se dobrarmos a largura da fenda para , teremos:
Como tínhamos , então agora teremos:
Passo 2
Letra b)
A capacidade de identificar duas fontes pontuais diferentes é definida pelo critério de Rayleigh, que diz:
“Dois objetos começam a poder ser distinguidos entre si quando a distância deles é tal que o máximo de difração de um coincida com o mínim de difração do outro”
Se considerarmos que seus máximos de difração tem mesma largura , então esse critério implica que a distância entre os máximos de difração tenham que ser igual a .
Passo 3
Agora podemos imaginar que o máximo central de difração de cada fonte se forma na reta que liga a fonte ao centro da fenda.
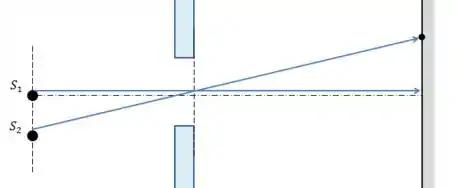
Por semelhança de triângulos, a distância entre as fontes e a distância entre os máximos de difração se relacionam na mesma razão que as distâncias entre as fontes e a fenda e entre a fenda e o anteparo.
Rearrumando:
Onde:
- (na condição do enunciado)
Resposta
Letra a)
Letra b)