Origem do Exercício
Qual é a distância mínima que deve separar dois objetos na Lua para serem resolvidos pelo telescópio espacial Hubble que tem um espelho de de diâmetro?
Considere a distância entre o Hubble e a Lua e o comprimento de onda da luz (luz violeta).
Passo 1
Vamos considerar que o espelho do Hubble é semelhante a uma fenda esférica. Se juntarmos isso com o critério de Rayleigh para a resolução de dois objetos, vamos ficar com:
Onde é o diâmetro do espelho e é a menor separação angular dos objetos que ainda permite que o Hubble os distingua.
Pelo enunciado:
Passo 2
Agora vamos fazer uma construção geométrica.
Podemos montar um triângulo retângulo usando os dois objetos que queremos resolver e a abertura angular
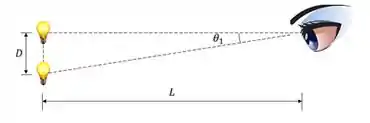
Isso nos diz que a distância mínima entre os dois objetos se relaciona com o ângulo por:
Sendo a distância do Hubble até a lua.
Como o ângulo é bem pequeno, podemos aproximar , e assim:
É a menor distância entre os dois objetos na lua tal que o Hubble consiga resolvê-los.