Difração
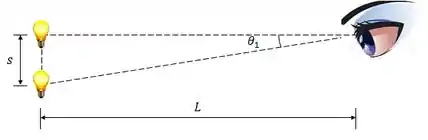
Duas fontes pontuais de luz estão afastadas de . Elas são vistas pelo olho a uma distância .
A abertura de entrada (pupila) do olho do observador tem um diâmetro . Se o olho é perfeito, o fator limitante para a resolução das duas fontes seria a difração.
Nesse limite, quão grande poderíamos fazer e ainda assim ver as fontes como entidades separadas?
Passo 1
De acordo com o critério de Rayleigh, dois objetos passam a ser distinguíveis quando a separação angular entre eles é dada pela equação:
Onde, para
Logo:
Resposta
Letra (d):
Exercícios de Livros Relacionados
(a) Estime quão próximo um carro se aproximando à noite em uma rodovia plana e retilínea de uma auto-estrada pode estar antes que seus faróis sejam distinguidos de um único farol de uma motocicleta. (
Explique por que a habilidade para distinguir os dois farois de um carro vindo a certa distancia emaior para o olho humano a noite do que durante o dia.Considere que os farois do carro que se aproxima
O diâmetro do radiotelescópio em Arecibo, Porto Rico, é 300 m. Qual é a menor separação angular entre os dois objetos que este telescópio pode detectar quando está ajustado para detectar microondas de
O radar de um cruzador usa um comprimento de onda de 1,6 cm; a antena transmissora é circular, com um diâmetro de 2,3 m. A 6,2 km do cruzador, qual é a distância mínima que deve existir entre duas lan
Os telescópios de alguns satélites de reconhecimento comerciais (como os usados para obter as imagens do Google Earth) podem resolver objetos no solo com dimensões da ordem de 85c m e os telescópios d