Luz de comprimento de onda de de uma fonte pontual distante incide normalmente sobre um anteparo com uma fenda de largura . O padrão de difração é observado numa tela a uma distância do anteparo.
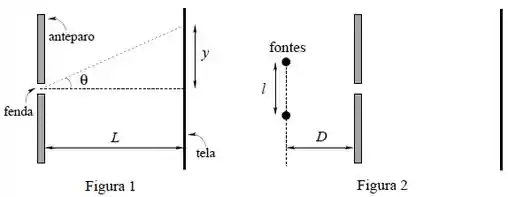
- Calcule a posição angular do primeiro e do segundo mínimos de difração com (use a aproximação ).
- Calcule a distância do primeiro máximo lateral de difração em relação ao centro da figura de difração (veja a figura 1). Use a aproximação de que um máximo lateral está situado à meia distância dos mínimos adjacentes.
- Considere agora duas fontes pontuais idênticas, não coerentes, emitindo luz desse mesmo comprimento de onda (), situadas à mesma distância da fenda e separadas por , conforme a figura 2. Determine a distância máxima para que essas duas fontes estejam minimamente resolvidas na tela.
Passo 1
Letra a)
A condição para a formação de mínimos de difração no anteparo é:
Onde
- é a largura da fenda
- é o comprimento de onda da luz
Temos então
O primeiro e o segundo mínimos correspondem a e respectivamente. Considerando a aproximação , nós obtemos:
Passo 2
Letra b)
Se considerarmos a aproximação de que o máximo de difração está exatamente no meio de dois mínimos, então para acharmos a posição do primeiro máximo lateral precisamos achar a posição do primeiro e segundo mínimos.
Pelo item anterior, temos que:
A posição de um dado mínimo pode ser calculada usando a tangente do ângulo:
Onde é a distância entre a fenda e o anteparo. Usando a aproximação , teremos:
Como o máximo vai estar no meio dos dois primeiros mínimos:
Ou seja, poderíamos ver apenas o ângulo médio entre os dois mínimos e achar a posição correspondente.
Passo 3
Letra c)
Como o máximo de difração está situado na reta que liga a fonte ao centro da fenda, podemos achar a distância entre os dois máximos:
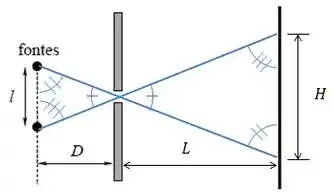
Onde é a distância entre os dois máximos.
Agora vem a sacada: Temos dois triângulos azuis, um com base e um com base . Os ângulos opostos à base dos dois são iguais, pois são opostos pelo vértice. Os outros dois ângulos de cada triângulo também são, porque e são paralelos.
Isso significa que os dois triângulos são semelhantes, e por isso suas bases e alturas são proporcionais umas às outras.
Passo 4
Pelo critério de Rayleigh, para ser possível resolver as duas fontes na tela, é necessário que o máximo de difração central de uma coincida com o primeiro mínimo de difração da outra.
Por isso, temos que ter . Substituindo na equação para
Resposta
Letra a)
Letra b)
Letra c)