Os dois faróis de um automóvel que se aproxima de um observador estão separados por uma distância de . Qual é:
- A separação angula mínima?
- A distância mínima para que o olho do observador seja capaz de resolvê-los?
Suponha que o diâmetro da pupila do observador é e use um comprimento de onda da luz de para a luz dos faróis.
Suponha também que a resolução é limitada apenas pelos efeitos da difração e, portanto, que o critério de Rayleigh pode ser aplicado.
Passo 1
Letra a)
A separação angular mínima para o olho humano distinguir os dois faróis vai ser aquela na qual o mínimo de difração de cada farol coincide com o máximo do outro.
Vamos avaliar para um dos faróis:
Onde é o diâmetro da pupila do observador e é o comprimento de onda da luz do farol. Resolvendo:
O que nos mostra que poderíamos ter usado a aproximação de pequenos ângulos diretamente e feito .
Passo 2
Letra b)
Com o ângulo encontrado, podemos encontrar a distância mínima entre o olho e os faróis a partir da tangente do ângulo.
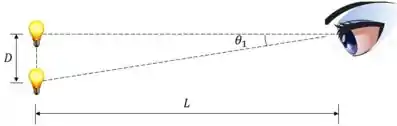
Pelo gráfico vemos que:
Que nos permite encontrar a distância mínima à qual o olho deve estar dos faróis para distinguí-los, usando a distância entre eles .
Rearranjando:
Resposta
Letra (a)
Letra (b)