Um satélite espião está em órbita circular a uma altitude de 650 km. Calcule o diâmetro da lente da câmera do satélite para que as fotografias tiradas com luz de comprimento de onda de 480 nm tenham uma resolução limite de 25 cm.
Passo 1
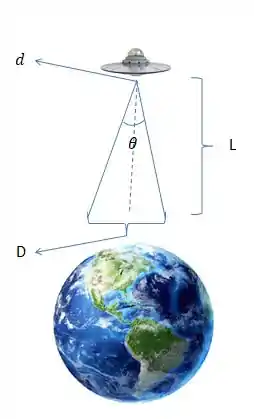
Podemos ver que essa questão se trata do que chamamos de critério de Rayleigh, vamos ver um desenho para podermos entender do que se trata o exercício.
Já com o desenho vamos compreender como ele se relaciona com a nossa fórmula.
Sabemos que a fórmula do critério de Rayleigh é
Em que é a lente da nossa espaçonave.
Mas só com esses dados não conseguimos resolver o nosso exercício.
Passo 2
Mas perceba o seguinte, lembra o que podemos fazer quando temos ângulos pequenos?
Podemos usar a relação que diz
Pela nossa figura podemos fazer a seguinte aproximação
Em que é a resolução máxima entre os nosso pontos, substituindo na nossa equação principal teremos a seguinte relação
Passo 3
Mas o nosso objetivo é determinar exatamente o tamanho na lente da espaçonave, ou seja, para isso podemos isolar o valor de
Agora basta relembrar os valores dados no enunciado
Substituindo teremos