Sejam um espaço vetorial munido de um produto interno e um subespaço de Se , e são vetores não nulos tais que , então o vetor de mais próximo de é:
Passo 1
Falaaa, blzz?? Bora para mais um problema dessa prova. Essa questão é uma aplicação e interpretação do que é uma projeção.
Nessa mesma prova, anteriormente, foi usado no enunciado a seguinte expressão:
Essa expressão é referente a projeção ortogonal de sobre , por definição, ou seja:
é o vetor de mais próximo de , agora basta a gente entender quem é esse tal de .
Passo 2
Bom, para fazermos esse problema, vamos lembrar um pouco o conceito de projeção ortogonal.
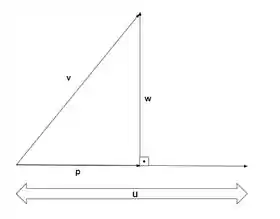
Nesse caso, temos que . A ideia de projeção, surge do fato de que . Ou seja, se temos as seguintes condições:
E daqui, tiramos que , por definição de projeção mesmo.
Além disso, da primeira equação, sabemos que
Logo, nosso objetivo é achar uma estrutura desse tipo, um vetor sendo igual a um cara menos alguém que é perpendicular a ele.
Passo 3
Agora, podemos aplicar isso no problema. Veja que temos o seguinte:
Ou seja, de forma análoga:
Agora, veja que , pois
Por isso , uma vez que .
Se você parar e refletir, vai ver que temos exatamente o “corpo” de projeção.
Então, unindo o que foi dito, podemos dizer que , e como queríamos achar isso, já chegamos na resposta. Bora para mais um problema??
Resposta
Letra D