Num triângulo , considere o ponto tal que , o ponto médio de , , e o ponto sobre o lado tal que o triângulo é retângulo em .
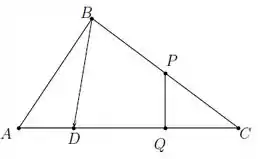
Organizando as informações
a) Escreva como combinação linear de e .
b) Se, em alguma base ortonormal tem-se e
b1) Calcule a área do triângulo .
b2) Determine as coordenadas do vetor na base .
Passo 1
a) Olhando pra figura, a gente sabe que
Agora temos em função de e :) vamos só dar uma arrumada pra ficar bonitinho:
Passo 2
b1) Lembra que a área do triângulo é metade do módulo do produto vetorial? Então
Os dados do enunciado falam pra gente que , então .
Primeiro vamos calcular o produto vetorial de com
Passo 3
Agora vamos calcular o módulo do produto vetorial:
Então, a área do triângulo vai ser
Passo 4
b2) O vetor vai ser a projeção ortogonal de sobre (veja isso pela figura), ou seja:
Antes de tudo bora encontrar os vetores e :
Sabemos do item anterior que . vai ser o oposto disso, ou seja, .
Como é o ponto médio de , temos que , logo:
Passo 5
Agora vamos calcular o vetor :
Resposta
a)
b1)
b2)