Exercícios de Projeção em Base Ortogonal - Lista de Exercícios Resolvida

Determine se ou para cada abaixo (as bases são ortogonais):

Determine se para cada abaixo (as bases são ortogonais):

Considere o espaço vetorial munido do produto interno usual . Seja uma base de dada por: e o operador de projeção sobre . Determine o operador .

Calcule a projeção do vetor na base formada pelos vetores e .

Calcule a projeção do vetor sobre o plano gerado pelos vetores

Em um espaço vetorial , o produto interno é dado por . Dados e , calcule a projeção de na base formada por e .

Dados:

Calcule a projeção do vetor sobre o plano gerado pelos vetores

Seja o vetor da reta gerada por que é o mais próximo do vetor . Então a soma de suas entradas, , vale:

Sejam um espaço vetorial munido de um produto interno e um subespaço de Se , e são vetores não nulos tais que , então o vetor de mais próximo de é:

Considere no o produto interno usual. Seja o subespaço .

b) Seja o operador projeção em Determine .

Considere o produto interno usual de . Calcule a projeção ortogonal do vetor no subespaço gerado pelo vetor .

Considere o produto interno , , , definido por .

Determine a soma das entradas da projeção ortogonal do vetor na direção do vetor .

Seja o plano gerado pelos vetores e . O vetor de que está o mais próximo possível do vetor é:

(a)

(b)

(c)

(d)

Seja uma base ortonormal do subespaço e seja , . Considere o vetor

(Aqui, denota o produto interno de e )

Pode-se afirmar que:

, onde denota a projeção ortogonal sobre .

é um conjunto ortogonal (mas não necessariamente ortonormal).

e são ortogonais.

.

Seja uma base ortogonal do seja o espaço gerado pelos dois primeiros vetores, e seja P a projeção ortogonal sobre W.

Então:

(I) é uma base de autovetores de P.

(II)

(a) Ambas as afirmações são falsas.

(b) Ambas as afirmações são verdadeiras.

(c) (I) é verdadeira e (II) é falsa.

(d) (I) é falsa e (II) é verdadeira.

Num triângulo , considere o ponto tal que , o ponto médio de , , e o ponto sobre o lado tal que o triângulo é retângulo em .

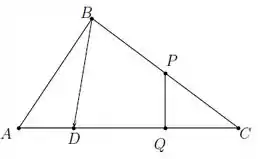
Organizando as informações

a) Escreva como combinação linear de e .

b) Se, em alguma base ortonormal tem-se e

b1) Calcule a área do triângulo .

b2) Determine as coordenadas do vetor na base .

Sejam tais que a projeção ortogonal de na direção de é igual a . O vetor pode ser qualquer um dos abaixo, COM EXCEÇÃO DE:

(a)

(b)

(c)

(d)

Considere o produto interno , , , definido por .

Determine a soma das entradas da projeção ortogonal do vetor na direção do vetor .

Sejam e Considere as afirmativas abaixo:

A projeção ortogonal de na direção de independe dos valores de e

A projeção ortogonal de na direção de independe dos valores de e

(a) Ambas são verdadeiras

(b)Ambas são falsas

(c) é falsa e é verdadeira

(d) é verdadeira e é falsa

Considere o produto interno usual de . Calcule a projeção ortogonal do vetor na reta que passa pela origem e possui a direção do vetor .

Considere o espaço vetorial e o produto interno . Dados e , determine a projeção ortogonal de em .

Seja o espaço vetorial formado pelas funções contínuas de em , e nele consideremos o produto interno . Seja o subespaço de dado por

Mostre que é uma base ortogonal de .

Encontre a função de que melhor aproxima a função

Obs.: É dado que

Seja o vetor da reta gerada por que é o mais próximo do vetor . Então a soma de suas entradas, , vale:

Considere o produto interno definido por . Determine a somadas entradas da projeção ortogonal do vetor na direção do vetor .