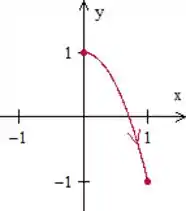
Para cada um dos seguintes pares de equações paramétricas, esboce a curva e determine sua equação cartesiana:
a) , ,
c) , ,
f) , ,
Passo 1
Podemos isolar o parâmetro na primeira equação e substituir na segunda, assim:
Temos a reta
Passo 2
Verificando intervalo para a curva da letra a:
não tem nenhuma limitação. Assim, .
Passo 3
Avaliando o sentido percorrido na curva da letra a: nós temos que ver se a derivada vai ser positiva ou negativa. Positiva, a função está crescendo. Negativa, a função está decrescendo.
Podemos observar que
Logo, a curva está “descendo”.
Passo 4
Esboçar a curva da letra a:
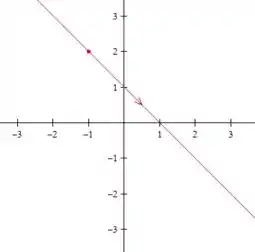
Como é real, ele varia de a e, nesse caso, nossa reta não tem nenhuma limitação. Quando , a curva passa pelo ponto que eu marquei ai.
Passo 5
Na letra c, vamos usar a relação fundamental da trigonometria
Assim, observamos que
Logo, também temos a reta .
Passo 6
Verificar o intervalo para a curva da letra c:
é uma função limitada, está sempre entre 0 e 1. Assim, e .
Passo 7
Avaliando o sentido percorrido pela curva da letra c:
Podemos observar que
Mas
Logo
E nesse intervalo, tanto o seno como o cosseno são positivos, então
Como o ponto inicial, ou seja, em vai ser
A curva começa em e o valor de vai aumentar.
Então ela está “subindo”.
Passo 8
Esboçando a curva da letra c
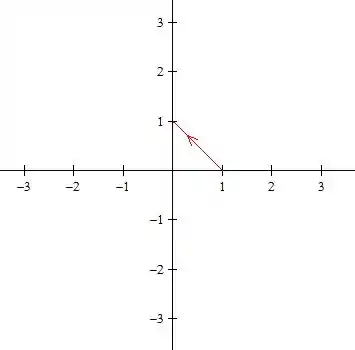
Passo 9
Na letra f pelo enunciado temos
E ele deu que
Então queremos achar uma relação de e
Lembrando das relações trigonométricas
E
Podemos usá-las para achar a função de e
Mas
Então
Temos a parábola
Passo 10
Avaliando o intervalo para a curva da letra f:
Vamos começar olhando o valor de
O seno indo de a , nos diz que o valor de vai de à .
Assim,
Passo 11
Vamos olhar o agora
Se
Então
Isso nós diz que o vai de à
Passo 12
A nossa curva vai ser
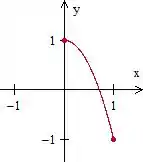
Passo 13
Vamos avaliar como varia essa função.
Como
Então
Isso nós diz que
Assim
E o valor de vai estar diminuindo.
A curva vai começar em
Então ela está “descendo”
Resposta
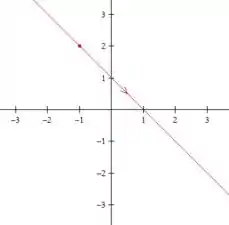
a)
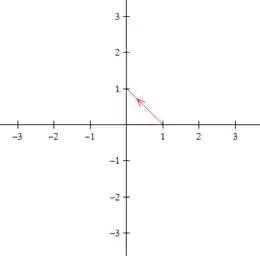
c)
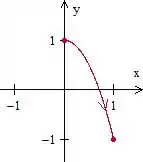
f)