UFAM – Cálculo 2 – Lista 1 – 2020 – Questão 2m
Esboce o gráfico da curva cuja equação vetorial é dada
m)
Passo 1
E aíí pessoal, tudo tranquilo?
Vamos pra mais um de funções vetoriais :P
Olha só, temos essa função vetorial:
E ela representa uma curva, certo? O que queremos aqui é esboçar essa curva fechou?
Podemos enxergar essa função vetorial assim:
Então vamos lá desenhar isso!
Passo 2
No nosso gráfico em 3D vamos ter
O eixo seeeempre vai valer , isso já é fato
Agora pra e podemos fazer:
Opa, então temos uma circunferência no plano . Ela vai ser centrada na origem e tem raio
Como é sempre igual a , essa circunferência vai estar deslocada até , assim:
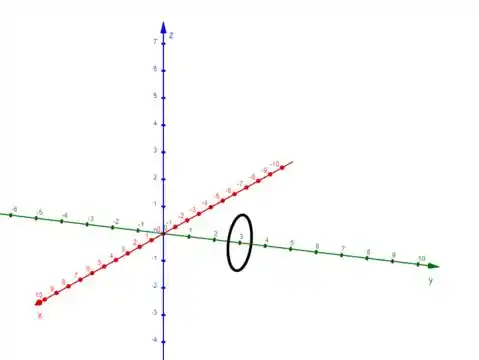
Sucesso demaisss!
Resposta
Imagem no passo 2