Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Aplicação de Funções Vetoriais, Arcos de Curvas

Ver Teoria
Exercício 131234567891011121415161718192021

Enunciado

UFAM – Cálculo 2 – Lista 1 – 2020 – Questão 2e

Esboce o gráfico da curva cuja equação vetorial é dada

e) α t = cos ⁡ t , 2 s e n t

Passo 1

Oiii, vamos pra mais uma?

Esse enunciado deu essa função vetorial:

α t = cos ⁡ t , 2 s e n t

E queremos desenhar a curva dela, ok?

Bem, o primeiro passo é lembrar que t ∈ R (uma dimensão), enquanto estamos indo para α t = cos ⁡ t , 2 s e n t , que tem duas dimensões

Então o desenho vai ter dimensão 1 + 2 = 3

E para entendermos como esse desenho vai funcionar, vamos acrescentar uma dimensão que vai ser o t . Então queremos desenhar isso aqui:

G = t , cos ⁡ t , 2 s e n t

Ou seja:

x t = t

y t = cos ⁡ t

z t = 2 s e n ( t )

Então bora!!

Passo 2

No nosso gráfico em 3D vamos ter

x t = t

y t = cos ⁡ t

z t = 2 s e n ( t )

Então, temos que x é um parâmetro que vai variar em todos os reais

E aí temos que y = c o s ⁡ ( x ) e z = 2 . s e n x

Vamos fazer:

4 y 2 + z 2 = 4 s e n 2 x + 4 c o s ² ( x )

4 y 2 + z 2 = 4 ∙ s e n 2 x + c o s 2 x

4 y 2 + z 2 = 4

y 2 + z 2 4 = 1

Isso é a equação de uma elipse no plano y z , em que o eixo maior está no eixo z

Passo 3

No plano y z temos uma elipse. Mas no eixo x temos que x vai variando em todos os reais

Então conforme o x vai variando, a elipse vai se movendo junto com ele, formando essa espiral:

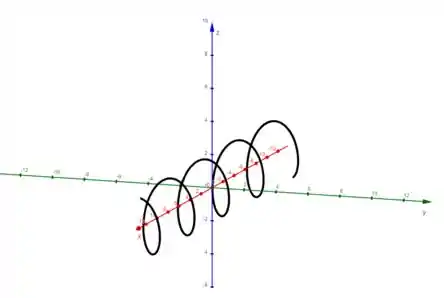
Sucessooo?

Resposta

Imagem no passo 3