UFAM – Cálculo 2 – Lista 1 – 2020 – Questão 2h
Esboce o gráfico da curva cuja equação vetorial é dada
h)
Passo 1
Oiii pessoal, tudo beleza?
Temos essa função vetorial:
E aí queremos esboçar a curva que ela ta representando, beleza?
O que temos aqui é:
Onde
Então vamos lá desenhar isso!
Passo 2
No nosso gráfico em 3D vamos ter
Então o vai variar em todos os valores reais positivos
Para e , podemos escrever
Então temos uma circunferência no plano com raio e centrada na origem
Mas como estamos em 3D, essa circunferência vai se movendo no eixo a medida que ele vai crescendo (lembrando que ele vai ser sempre positivo, por definição do enunciado). Então, temos essa espiral ao longo do eixo :
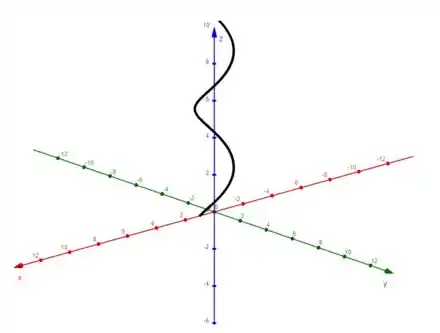
E é isso aíí
Resposta
Imagem no passo 2