UFAM – Cálculo 2 – Lista 1 – 2020 – Questão 2f
Esboce o gráfico da curva cuja equação vetorial é dada
f)
Passo 1
Faaaala galera, vamos lá pra mais uma de gráficos
Temos essa função vetorial:
E aí queremos esboçar quem é a curva que essa função está representando, belezinha?
Bem, o primeiro passo é lembrar que (uma dimensão), enquanto estamos indo para , que tem duas dimensões
Então o desenho vai ter dimensão
E para entendermos como esse desenho vai funcionar, vamos acrescentar uma dimensão que vai ser o . Então queremos desenhar isso aqui:
Ou seja:
Então bora!!
Passo 2
No nosso gráfico em 3D vamos ter
Então, temos que é um parâmetro que vai variar em todos os reais
O vai variar juntinho com o . E o vai ser , ou hahahaha
Então basicamente, vamos ter uma senoide em que só vai ser aplicada quando e forem iguais
Passo 3
Temos que é uma reta identidade entre e : eles são sempre iguais
E aí a nossa senoide vai estar em cima dessa reta identidade:
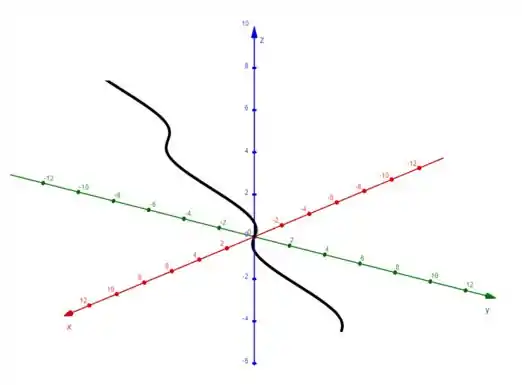
Sucessooo?
Resposta
Imagem no passo 3