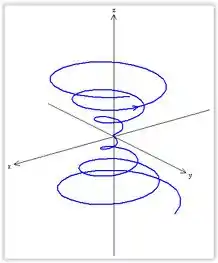
Seja a curva parametrizada:
Faça um esboço da trajetória percorrida pela partícula.
Passo 1
Similar a questão anterior vou fazer um passo zerinho, por que aqui a gente também consegue esboçar sem fazer contas.
Observa que temos
Bom, com isso a gente sabe que no plano nós vamos ter a circunferência pela relação entre o seno e cosseno, certo? No entanto se você for observar eu tenho t multiplicando o seno e cosseno. Isso faz com que quando nós não teremos a circunferência. Conforme o t vai crescendo, mais aumenta essa circunferência no plano .
Vamos ter então isso
Mas não se preocupa! Se você não pegou essa explicação, segue a explicação normal haha Isso daqui seria só pra te mostrar que a gente consegue ter uma noção analisando os termos, sem necessariamente fazer várias contas.
Passo 2
Identificar curva:
Pelas equações paramétricas da curva, podemos ver que
Logo:
Então essa é uma helicoidal cônica.
Passo 3
Avaliar :
Logo, a curva “sobe” com o aumento do parâmetro
Passo 4
Verificar intervalo e ponto inicial:
Como t é real, ele varia de a . Quando , a curva passa pelo ponto:
Passo 5
Esboçar curva:
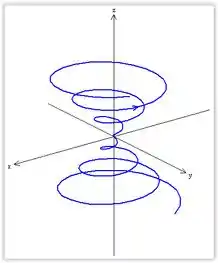
Resposta