UFAM – Cálculo 2 – Lista 1 – 2020 – Questão 2d
Esboce o gráfico da curva cuja equação vetorial é dada
d)
Passo 1
Oiii galera!!
Olha só, temos essa função vetorial:
E queremos fazer o desenho da curva dela
Bem, o primeiro passo é lembrar que (uma dimensão), enquanto estamos indo para , que tem duas dimensões
Então o desenho vai ter dimensão
E para entendermos como esse desenho vai funcionar, vamos acrescentar uma dimensão que vai ser o . Então queremos desenhar isso aqui:
Ou seja:
Então bora!!
Passo 2
No nosso gráfico em 3D vamos ter
Então, temos que é um parâmetro que vai variar em todos os reais
O vai ser igualzinho esse e o vai ser
Portanto, a nossa superfície vai ser a intersecção entre as superfícies e
Para esboçar essas superfícies, podemos enxergar primeiro como duas dimensões e depois expandir para 3 dimensões
Por exemplo, o no plano fica assim: (a função só que vista no plano )
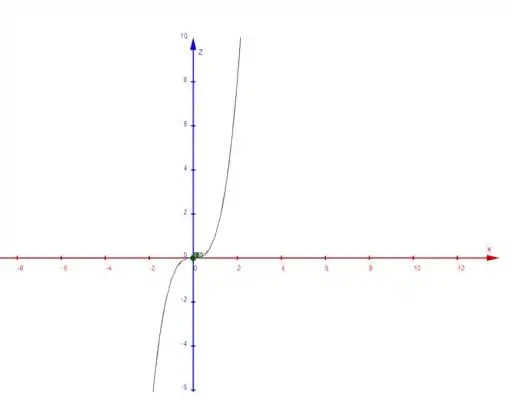
E aí expandindo para 3 dimensões, acrescentando o eixo , temos
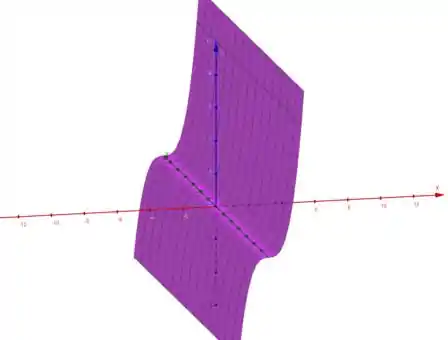
E aí fazemos o mesmo para no plano
Passo 3
Nossa superfície vai ser a intersecção dessas duas superfícies:
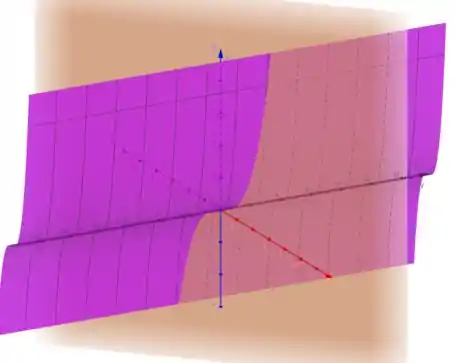
Que vai ficar assim:
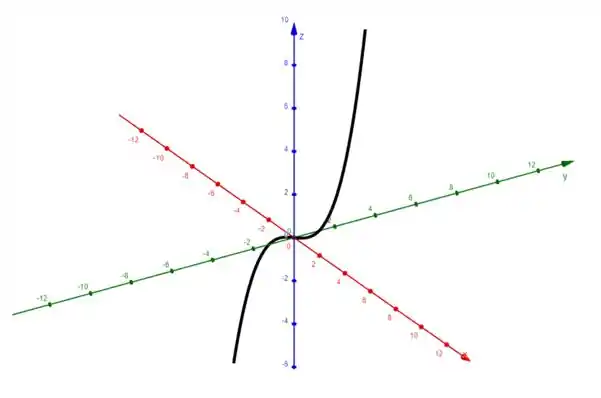
Arrasamos!!
Resposta
Imagem no passo 3