Exercícios Resolvidos de CL e DL de Polinômios e Matrizes

Exercício 14 1 2 3 4 5 6 7 8 9 10 11 12 13 15

Enunciado

USP, Sem Campus, Álgebra Linear 2, Psub - 2017, Questão 10

Sejam e considere a matriz:

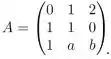
Se o polinômio característico de for,

então:

(a);

(b)

(c)

(d)

(e)

Passo 1

Fala pessoal, tudo beleza? Vamos para mais uma questão de Algelin. Nosso objetivo é descobrir as entradas da matriz . Para isso, nós temos o polinômio característico da matriz. Então bora resolver.

Como

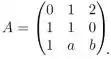
seu polinômio característico é, Por definição,

Contudo, o enunciado diz que o polinômio é

Ora, temos aqui uma igualdade entre polinômios. Isso quer dizer que os coeficientes que acompanham as potências de tem que ser os mesmos em ambos os polinômios.

Dessa forma, temos que ter

Resolvendo o sistema acima, descobrimos que

valores presentes na alternativa

Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊

Resposta

Exercícios de Livros Relacionados

Sejam L 0( t ) ,L 1( t ) , . . .,L n ( t ) Os polinômios de Lagrange correspondentes a ( t o ,t 1 , . . . ,t n ) . Provar que L 0( t )+L 1( t )+ . . .+L n ( t )= 1 e que t=t 0 L 0 ( t )+t 1 L 1 ( t )+

Exprimir o polinômio f ( t ) como combinação linear dos polinômios de Lagrange do exercício1 nos seguintes casos:a) f ( t )=t 2 b) f ( t )=t 2+t+1 c) f ( t )=1

Sejam a ,b ,c ,d números reais distintos dois a dois. Provar que existe um polinômio de grau menor ou igual a 2 tal que: f - 1 = a ,f 1 =b ,f 3 = c ,f O =d se, e somente se, 3 a+6 b-c-8 d=0 .

f ( t ) = a o + a 1 t + + . . . + a m t m E uma matriz A , indica-se por f ( A ) a matriz a 0 I b + a 1 A + … + a m A m ·. Calcular f ( A ) nos seguintes casos:

Determinar os polinômios de Lagrange correspondentes aos valores t 0 , t 1 , t 2 , t 3 , t 4 =( 0 ,1 ,2 ,3 ,4 ) e exprimir o polinômio f ( t )=t 4+t 3-t 2-t+1 como combinação linear deles. Repetir o e