USP– Cálculo 1 – Lista 2 – Questão 5.1
Calcule
Passo 1
Oi, tudo bem? Essa questão parece complicada, mas vou descomplicar para você! O problema deu essa integral
E pediu para calcularmos!
Mas como resolver isso?
Precisamos lembrar da paridade de funções! Uma função é considerada par quando
E ímpar quando
Tá, mas o que isso tem a ver com a área! TUDO!
Quando temos uma função ímpar e limites de integração simétricos, a área é zero! Isso porque a área antes do eixo é igual a área depois do eixo e elas se cancelam!
Lembrando que não existe área geométrica negativa, o que estamos calculando é uma integral que podemos representar geometricamente por uma área!
Se a função for par, podemos calcular a área de metade do intervalo apenas, pois as duas serão iguais!
Beleza?
Nossa missão é analisar a paridade dessa função e descobrir que área estamos lidando
É isso! Bora lá?
Mas relaxa, vou fazer passo a passo com você!
Passo 2
Vamos começar olhando nossa função
Trocando por temos
Ou seja!
Beleza?
Temos uma função ímpar! E portanto a integral que tem limites simétricos entre e é zero!
Passo 3
Ainda podemos ver o esboço do gráfico dessa função
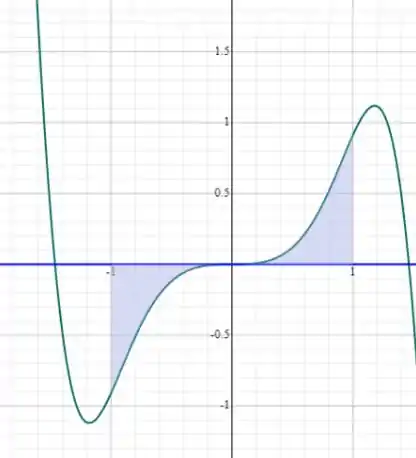
A área à esquerda é igual à da direita, mas com sinal trocado pois está abaixo do eixo dos ! Isso significa que somando as duas temos zero!
Show! E é isso pessoal! Espero ter ajudado!