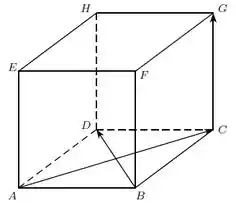
O paralelepípedo da figura é um cubo de aresta .
a) Mostre que é uma base ortonormal.
b) Escreva na base .
Passo 1
a) Para que esses vetores formem uma base ortonormal, devem ter módulo 1 e serem ortogonais entre si.
Primeiro vamos analisar e . Esses vetores são as diagonais da base do cubo que tem lado . Como são as diagonais do quadrado , são ortogonais entre si. Além disso, seu tamanho vale .
Agora, se formos calcular o módulo dos dois primeiros vetores de teremos:
Boaa! Agora só falta analisarmos o terceiro vetor!!
Passo 2
O vetor é uma aresta do cubo e está perpendicular à base dele, ou seja, já temos que é perpendicular aos 2 vetores anteriores :D
Essa aresta mede , logo, o módulo do vetor dado em vai ser
Agora simm, temos que os 3 vetores são ortogonais entre si e todos possuem módulo 1 :) Logo, é uma base ortonormal!!
Passo 3
b) Nosso objetivo aqui é escrever o vetor em função dos vetores da base .
Temos que
Substituindo e pelos seus vetores congruentes:
Isso é a mesma coisa que
(Repare que se cortarmos em cima e embaixo teremos a mesma equação anterior)
Logo, em função dos vetores de :
Resposta
a) Demonstração.
b)