Em um tetraedro considere os vetores , e . Determine as coordenadas dos pontos , , e no sistema de coordenadas construído com a base e origem .
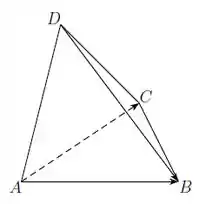
Passo 1
O problema quer as coordenadas na base com origem . Então vamos visualizar a figura de outra maneira, o que a gente tem é basicamente algo assim
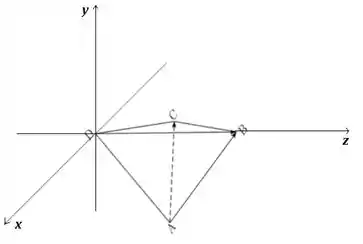
Logo de cara, a gente já consegue saber que (já que ele é a própria origem) e . Então vamos usar esses dois pontos para descobrirmos e .
Passo 2
Vamos brincar com os vetores. Como queremos os pontos e na origem , vamos encontrar e em função dos vetores da base .
Sabemos que
Escrito na base , isso é equivalente a
Logo
Agora para :
Então,
Resposta
Exercícios de Livros Relacionados
12. É dada uma base ortonormal com o produto interno euclidiano. Use o teorema 6.3.2b para encontrar o vetor de coordenadas de w → em relação a essa base.(a) w → = 3,7 ,u → 1 = 1 2 , - 1 2 , u → 2 = 1
11. (a) Mostre que os vetores v → 1 = 1 , - 2,3 , - 4 ,v → 2 = 2,1 , - 4 , - 3 ,v → 3 = - 3,4 , 1 , - 2 ,v → 4 = 4,3 , 2,1 Formam uma base ortogonal de R 4 com produto interno euclidiano.(b) Use o Teo
13. É dada uma base ortonormal com o produto interno euclidiano. Use o teorema 6.3.2b para encontrar o vetor de coordnadas de w → em relação a essa base.(a) w → = 2,0 , 5 , u → 1 = 2 3 , 1 3 , 2 3 , u
8. Verifique que o conjunto de vetores 1,0 , 0,1 é ortogonal com o produto interno u → , v → = 4 u 1 v 1 + u 2 v 2 de R 2 e converta-o num conjunto ortonormal normalizando seus vetores.
9. Verifique que os vetores: v → 1 = - 3 5 , 4 5 , 0 , v → 2 = 4 5 , 3 5 , 0 , v → 3 = 0,0 , 1 Formam uma base ortonormal de R 3 com o produto interno euclidiano. Depois, em cada parte, use o Teorema