Probabilidade Conjunta – Variáveis Aleatórias Bidimensionais
Uma moeda equilibrada é lançada duas vezes. Uma cara é associada ao número 1 e uma coroa, ao número 0. O par de variáveis aleatórias é definido como:
resultado do primeiro lançamento + resultado do segundo lançamento
resultado do primeiro lançamento − resultado do segundo lançamento
(a) Encontre a função de probabilidade conjunta do par
(b) Encontre as distribuições marginais de e .
(c) Calcule a covariância entre e .
(d) e são independentes? Justifique sua resposta.
Passo 1
a)
Vamos primeiro organizar todos os valores possíveis que e podem assumir. Começando pelo , que é a soma dos resultados dos dois lançamentos:
Então pode ser 0,1 ou 2.
Agora , que é a subtração dos resultados dos dois lançamentos:
Então pode ser -1, 0 ou 1. Show, agora vamos resolver nossos itens!
Passo 2
Estamos num problema com V.A.s Bidimensionais Discretas e pediram uma função de probabilidade conjunta pra gente. Como assim?! A questão tá pedindo pra gente construir aquela tabela com as probabilidades conjuntas de e Lembra dela?
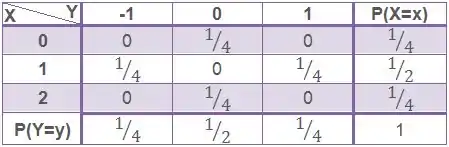
Temos que completar o corpo dessa tabela então com os valores das probabilidades conjuntas. Vamos começar com o primeiro quadro, quando e , ou seja:
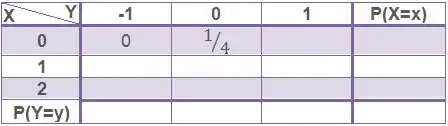
Nosso é 0 quando tiramos duas coroas, e nosso é -1 quando tiramos uma coroa e uma cara. Então nunca vai poder ser 0 quando é -1, nem vice-versa, porque são cenários diferentes! Então:
E quanto seria ? X e Y são zero ao mesmo tempo quando tiramos duas coroas! Então é possível de acontecer, e pra saber as chances, basta calcularmos a probabilidade de saírem duas coroas em dois lançamentos de uma moeda:
Então:
Botando essas probabilidades na nossa tabela:
Seguindo o mesmo raciocínio vamos calcular o resto das probabilidades conjuntas:
impossível acontecer
impossível acontecer
impossível acontecer
impossível acontecer
Agora põe essa galera toda na nossa tabela!
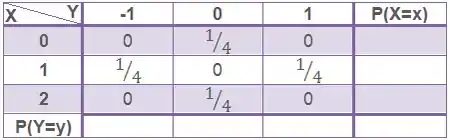
Passo 3
b)
Agora ele quer as probabilidades marginais, ou seja, essa última linha e última coluna que deixamos em branco na nossa tabela. E como calculamos elas?
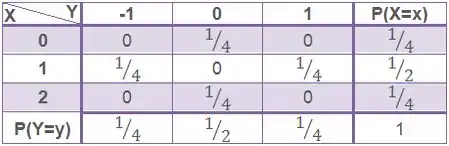
Para achar uma marginal ao final de uma linha, basta somarmos todas as probabilidades conjuntas dessa linha. E para achar uma marginal ao final de uma coluna, basta somarmos todas as probabilidades conjuntas dessa coluna:
Para :
E da mesma forma pra
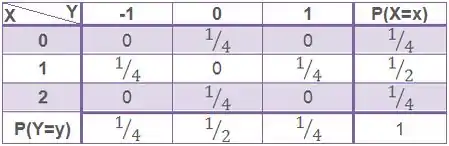
Relembrando que aquele 1 no cantinho é a probabilidade total, e sempre é 1!
Passo 4
c)
A Covariância é dada por essa fórmula aqui:
Vamos calcular nossa esperança conjunta :
Pra poupar nosso tempo, vamos ignorar as colunas e linhas da tabela onde ou valham zero, ou então quanto a probabilidade conjunta for zero, porque esses termos vão resultar uma soma zero no nosso somatório, o que não muda nada!
Agora vamos calcular as esperanças individuais:
Dessa forma nossa Covariância de e é:
Passo 5
d)
Para nossas variáveis serem independentes, as probabilidades conjuntas têm que ser iguais as probabilidades marginais associadas a ela! Ou seja:
E isso tem que ser verdade para TODAS as probabilidades conjuntas da tabela! Vamos testar.
Para nossas variáveis serem independentes, as probabilidades conjuntas têm que ser iguais as probabilidades marginais associadas a ela! Ou seja:
E isso tem que ser verdade para TODAS as probabilidades conjuntas da tabela! Vamos testar:
Resposta
Letra b)
Letra a)
Letra c)
Letra d)
Não são independentes.