USP probabilidade e estatística probabilidades PSUB 2019
Considere a distribuição conjunta das variáveis aleatórias a seguir.
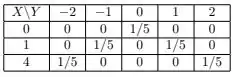
Pode-se afirmar sobre :
a) ;
b) ;
c) , logo são independentes ;
d) São dependentes.
Passo 1
Fala pessoal. Tudo beleza? Vamos para mais uma questão. Nosso objetivo é verificar quais afirmações são verdadeiras, e para isso, nos é dada a distribuição conjunta de
Passo 2
Vamos lá, pessoal. Antes de verificarmos as afirmações. Vamos obter as distribuições MARGINAIS de . Mas como se faz isso mesmo?
Bem, para o caso discreto, a marginal de é dada por:
Ou seja, ficamos um valor de e fazemos a soma nos demais valores de .
De forma análoga, a marginal de é dada por:
Com isso em mente, vamos calcular as marginais de
; ; (somamos a linhas da tabela de distribuição)
; ; ; ;
(somamos as colunas da tabela de distribuição)
Passo 3
Agora que calculamos as distribuições marginais, podemos começar a verificar as afirmações.
Vamos começar pela letra a)
Queremos verificar se . Bem a definição de covariancia é:
Sendo assim, precisamos calcular
Vamos começar pela
(pela definição da esperança)
Opaaa, já não precisamos mais calcular , pois como
então
Passo 4
Vamos calcular .
Para isso, vamos verificar todos os possíveis valores de e somar as probabilidades para cada caso.
Ocorre se então
Como queremos calcular não precisamos verificar o caso onde , já que não terá influência na esperança.
Juntando os resultados acima temos que
😊
Então temos que
Passo 5
Pronto chegamos a conclusão que . Então a letra b) é verdadeira.
Falta verificarmos se são independentes, mas essa é fácil de verificar.
Se forem independentes. Então
Mas tome . Então
(ao consultarmos a tabela)
(usando as marginais que calculamos no passo 2)
Logo
O que implica que são dependentes.
Finalmente, terminamos mais uma questão. Chegamos a conclusão que as letras b) e d) estão corretas. Espero que os passos tenham ficado claros. E não se esqueçam, covariância igual a zero não implica independência, mas independência implica covariância nula.
Até a próxima questão!! Bons estudos 😊 .
Resposta
b) e d)