Sejam e duas v.a.’s discretas cuja função de probabilidade conjunta é expressa por:
- Constante para que para que seja uma função de probabilidade das variáveis aleatórias e .
- Densidade condicional de dado .
- Podemos afirmar que e são independentes? Justifique sua resposta.
Determine a constante para que seja uma função de probabilidade das variáveis aleatórias e .
Passo 1
Vamos começar resolvendo a letra a) da questão. É importante tomarmos cuidado pois as contas decorrentes desta letra serão fundamentais para que consigamos resolver todo o resto da nossa questão!
Bom, para que a função seja uma função de probabilidade, a soma das probabilidades das distribuições marginais deve ser igual a 1. Isto é,
Confuso né? E então, o que precisamos fazer?
Vamos começar assumindo que a nossa é uma função de probabilidade conjunta. Agora que assumimos isto, vamos montar uma tabela para descrever os valores de nossa . Mas calma, até qual valor de iremos montar a tabela? Porque pelo enunciado da questão eles variam de 2 até infinito.....
E aí??????? Bom, vamos montar até o valor 4, depois vocês irão perceber que é desnecessário continuar.
Portanto, temos a seguinte tabela:

Vocês conseguem perceber que a cada vez que a gente aumenta o valor de o denominador fica maior? Consequentemente, o número final fica cada vez menor. É por causa disso que podemos parar por aqui no cálculo.
Passo 2
Agora que calculamos o valor da probabilidade de cada uma das combinações de e para valores de e variando entre e , o que precisamos fazer agora? A resposta para esta pergunta é: precisamos determinar dois parâmetros que a questão nos deu: as distribuições marginais e .
A ideia por trás da distribuição marginal é simples. Lembra que estamos com uma distribuição conjunta ? Então, imagina aí: o que aconteceria se a gente fixasse um determinado e variasse o ? Se somarmos todas essas probabilidades, obteríamos uma probabilidade deste nosso evento acontecer.
Pronto, esta é uma ideia resumida da distribuição marginal. Mas sim, o que importa é como calcular. E como fazemos isto? Aí já é mais fácil ainda! É só nós somarmos as linhas (colocando o resultado final na última coluna a direita) e somarmos as colunas (colocando o resultado final na última linha abaixo).
Por fim, é basicamente acrescentar uma linha e uma coluna a tabela dada na questão. Portanto, temos:
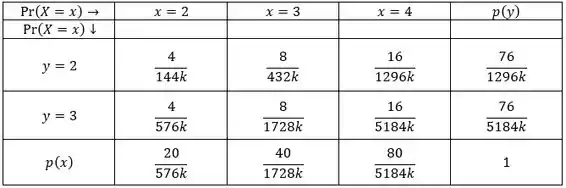
E agora? O que devemos fazer? Eu digo a vocês que a chave para resolvermos a questão continua na tabela. Em especial, na última linha e última coluna. Mais especial ainda naquele belo número 1.
Para que a nossa seja uma função de probabilidade, significa que a soma das probabilidades das distribuições marginais (aquela última linha e última coluna), tem que dar igual ao número 1.
Vamos utilizar a identidade acima para calcularmos o valor de . Portanto,
Então, basta descobrirmos qual o valor de que satisfaz a seguinte relação:
Portanto, o valor aproximado de que torna uma função de probabilidade de variáveis e é aproximadamente .
Passo 3
Agora precisamos calcular a densidade condicional de dado . Portanto, precisamos aplicar a seguinte relação:
Então, temos que revistar a nossa tabela:
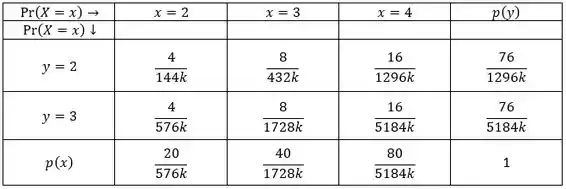
Percebam que o valor de não importa para este caso.
Agora, é só substituirmos os valores da tabela na nossa fórmula. Portanto, se calcularmos a densidade condicional para cada um dos casos, vamos obter:
Passo 4
Para finalizarmos a questão, precisamos responder ser os eventos e são independentes. Vamos resolver esta questão pelo cálculo da covariância. Se , então os eventos são independentes. Mas, para isto, teríamos de calcular uma série de parâmetros, o que não é o foco aqui!
Mas o que importa mesmo é como calcular a covariância? E aí? Como fazer?
Para isto, podemos aplicar a seguinte relação:
Mas o que seriam estas funções e ? Elas são as esperanças (a mesma ideia de uma média). Para calcularmos as esperanças, podemos utilizar as seguintes relações:
Conseguem ver o motivo de termos obtido as distribuições marginais? Para calcularmos e precisamos das probabilidades e . Então, nós nos adiantamos no problema!
Relembrando, temos a seguinte função de probabilidade (já substituindo ).
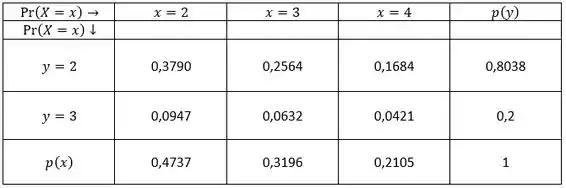
Percebam que qualquer diferença nos valores se deve pela aproximação.
Agora, vamos calcular primeiramente as esperanças e . Portanto,
Simples. Para calcular , pegamos o valor de cada e multiplicamos pelo seu respectivo e depois somamos todos os termos. E o mesmo ocorreu para .
Agora, vamos calcular . É importante tomarmos cuidado pois temos um somatório dentro do somatório. A ideia é trabalhar do somatório de dentro para o de fora. Então, vamos começar a expandir estes somatórios:
Agora, vamos analisar o valor de cada separadamente (seria o respectivo a cada linha da nossa tabela). Para , temos:
Já para , temos:
Portanto, a esperança é:
E agora podemos finalmente calcular a nossa covariância que é dada por:
Bom, apesar da covariância diferenciar um pouco de zero, pode-se perceber que ela tende a zero. Isto ocorreu por causa dos valores utilizados, pois eles estavam arredondados. Portanto, no final, sabemos que e os parâmetros são independentes.
Resposta
- ;
- As variáveis são independentes.